遥远的太阳

和地球之间的平均距离大约是1.5亿千米，这成为第一把尺子，称为“天文单位”。这是一把小尺子。更大一点的尺子叫“光年”。光是世界上速度最快的，约为30万千米/秒，1秒钟就可以绕地球7圈多。光1年要走大约10万亿千米，光年成为一把大尺子。还有一把更大一点的尺子叫“秒差距”。1秒差距等于3.26光年，差不多等于32万亿千米。

　　太阳是距离我们最近的恒星，它的距离是8光分19光秒。除了太阳以外，离我们最近的恒星是半人马座的比邻星，距离是4.22光年。人们比较熟悉的牛郎星为16光年，织女星是25光年。北极星的距离则为680光年。在银河系中离我们最远的恒星距离大约8万光年。河外星系中的恒星，离我们则有几亿甚至一二百亿光年。

　　我们生活在一个三维空间。我们肉眼所看到的星座则是恒星在天球上的投影，是两维空间的图像。如果我们不知道恒星的距离，那么就不能知道恒星在空间的真实分布、它们的运动速度和发射电磁波的真实强度。

　　恒星离我们那么遥远，怎样才能测量出它们的距离呢？比较近的恒星可以用三角的方法进行测量，这种方法是1838年由德国天文学家贝塞尔首创的。这种测量恒星距离方法的原理，与我们在地面上测量远处某点的距离的原理，是相同的。譬如，我们要测量远处的一座高塔的顶到我们的距离。可以先确定相隔一段距离的两个点A和B，测出它们之间的准确距离，作为基线。然后分别从A点和B点去观测塔尖C的方向，∠CAB和∠CBA的大小都可以使用普通的测绘仪器量出。在三角形ABC中，知道了两个角和一夹边，就可以求出它的其他边长和高了，即能够得到塔顶到我们的距离。基线AB相对的角叫做“视差角”，在天文学中通常用字母π来表示。显然，视差角π的大小与基线AB的长短有关，AB越长视差角π也越大。而且，对于已经固定的基线AB来说，要测距离的C点越远，视差角π就越小。视差角越小，测得的距离的精度就越差。

　　测量不太远处的恒星，我们可以把地球绕太阳运动轨道的直径作为已知距离的基线。地球绕太阳一周的时间是一年，绕行半周就是半年，地球正好处在地球轨道直径的两端。处在地球轨道直径的两端时分别观测同一颗恒星，其方向是不同的，也就是可以测出它的“视差角π”。由视差角π和地球的轨道直径（3亿千米），便可以计算出恒星的距离。天文学家利用三角视差法测定了大约7000颗较近恒星的距离。这些恒星的距离大约都在二三百光年之内。

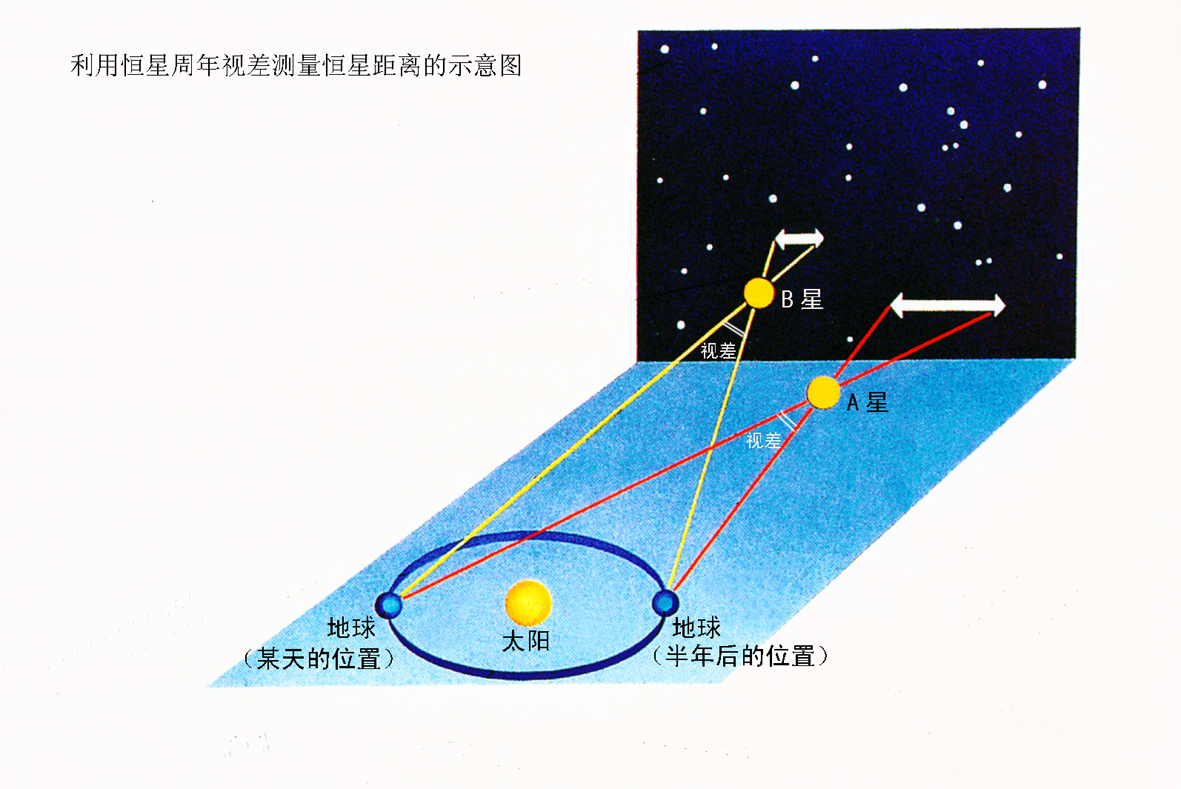
　　对于那些距离超过二三百光年的恒星，因为它们的视差角太小了，小于0″.01，根本没有办法将它们则得准确，所以只能寻找其它方法。其中一个著名的方法是利用造父变星的周光关系来推算遥远天体的距离，造父变星因此而获得了“量天尺”的美誉。
< 1 > < 2 >

设为首页 | 加入收藏 | 广告服务 | 友情链接 | 版权申明