南京师大附中江宁分校 叶军
作为一种特殊的相似,八年级的数学教材新增了“位似图形的作法”,对学生能力并不作过高要求,学生的感受也是“见山是山,见水是水”,除了学会作图之外,对于位似变换未有深刻的理解。但是位似作为一种重要的几何变换,在实际问题中有着不可替换的地位。因此本文介绍几个应用位似作图的例子,供比较学习之用。
先看一个问题:如何在一张三角形纸片上剪出一个最大的正方形?
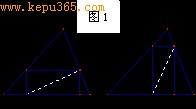
剪出一个矩形是容易的,如图1。但是要保证DEFG是一个正方形确实不易。如果尝试直接在边上取点,矩形DEFG不是太高就是太扁,总不能恰如其分。如果设BC=a,BC边上的高为h,可以算出正方形DEFG的边长为ah/(a+h),这么长的线段是可以作出来的,在此意义下,该问题已经解决。但这个解法依赖于线段的度量值,手工作图误差较大,且并不直接,因此有必要寻找一个更好的解法。
我们观察这个图形,可以发现矩形DEFG其实完全决定于直角三角形DEF,因此只要使得DEF为等腰直角三角形即可解决问题。
在纸上任意画一个等腰直角三角形是容易的,但是要把它的三个顶点分别落在已知三角形的三条边上(此情形称为“内接”)却有点困难。但如果这个问题解决了,意味着开始的问题也能解决,因此我们转向一个新的问题:在△ABC上作一个内接△DEF,使得三条边与已知△PQR的三边分别平行。
[1] [2] [3] 下一页
