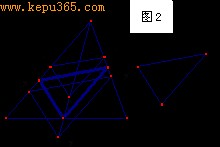
开始也要尝试,如图2,我们先在AB、AC上取D、E,使得DE∥PQ,再作DF∥PR,EF∥QR,可以发现,F点未必正好落在BC上,这是问题的关键。如果多试几次可以发现,这样的F都在由A出发的一条射线上,且△∽△,因此△和△是以A为位似中心的位似图形。根据位似图形的性质,对应点都在经过位似中心的直线上,因此记AF1与BC的交点为F,从F作DF∥PR,EF∥QR,交点分别在AB、AC上,△DEF就是所求,见图中粗线。
以上分析过程的关键是看到了所有的尝试答案都是关于A点的位似图形,但其中只有一个是我们需要的,这是问题的本质。如果我们调整△PQR为等腰直角三角形,且PQ∥BC,PR⊥BC,则开始的问题迎刃而解。
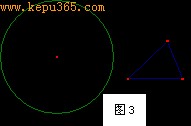
再看一个问题:已知圆P和△ABC,求作圆P的内接△DEF,其三边分别与△ABC的三边平行。
如果尝试刚才的方法分析这个问题,你会发觉在此行不通了,因此必须另寻他路。我们采用的思路是几何证明中的“分析法”,即先假设答案已经有了,它必须具备什么性质,最后我们可以根据该性质作图。
如果图形已经作出,如图4。那么△ABC和△DEF有个位似中心O,这两个三角形的外接圆也关于O位似,且有相同的位似比。因此,我们不妨先作出△ABC的外接圆Q,再作出两个圆的位
上一页 [1] [2] [3] 下一页
