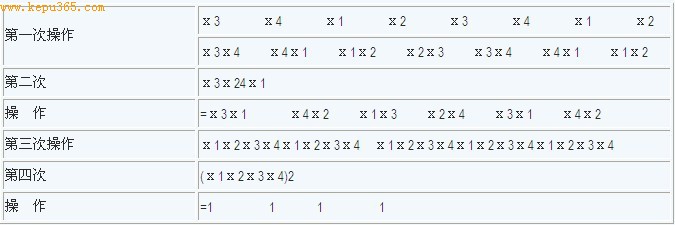
由上表可见,经第4次操作后,符号皆为正,故4枚棋子都应放黑子。
用数学归纳法可以证明,一般情况下,若圆周上原来摆着2n枚棋子,最多操作2n次后一定全剩下黑子。
例4有11只杯子都口朝上放着,然后将它们任意翻偶数只算一次操作(翻过的也可以再翻)。证明:无论操作多少次,都不能使11只杯子都口朝下。
解将口朝上的杯子记为1,口朝下的记为-1,然后计算每操作一次后11只杯子乘积的正负号:
开始,11只杯子都口朝上,所以乘积的符号为:111=1。
当翻动n个杯子(n为偶数且n≤10)使其口朝下时,乘积的符号为:
111-n·(-1)n=1·1=1
继续讨论可知,无论n是小于11的什么偶数,乘积的正负号均为正,而11只杯子都口朝下时,乘积为(-1)11=-1,故不可能办到。
本问题的一般结论是:奇数个杯子每次翻动偶数个或偶数个杯子每次翻动奇数个,都不能使所有杯子都口朝下。
3抽屉原理抽屉原理是证明“存在性”问题的有力工具,其最基本形式是:将n+1(或更多)个元素任意放入n个抽屉中,则至少有一个抽屉中至少有两个(或更多)元素。抽屉原理的正确性简单而显然,但具体运用并不容易,困难之处在于怎样设置抽屉,把一个实际问题转化为抽屉原理问题。
例5世界上任意6个人中,总有3个人,或彼此都认识,或彼此都不认识。
这是有名的Ramsey问题,要用抽屉原理来解。
对6个人中的任一个人,不妨设为A来说,除A外的其余5人可分为同A相识或不同A相识两类(即两个抽屉),由抽屉原理可知,至少有一类中至少有3个人。分别讨论如下:
如果同A都认识的那一类中至少有3人,若有3人互相都不认识,则结论成立;否则至少有两个人互相认识,而这两人又都同A认识,故有3人互相认识,结论也成立。
如果同A都不认识的那一类中至少有3人,若其中有3人互相认识,则结论成立;否则,至少有两人彼此不认识,但这二人又都与A互不认识,故这时有3人互相不认识,结论也成立。
此问题也可以用染色法来证明:
在平面上用A1,A2………A6来代表6个人,设它们无三点共线。将互相认识的两人连一条红线,否则连一条蓝线。问题就转化为:在这15条连线中要证明至少有一个同颜色的三角形。
证明:考虑由A1出发的5条线,因为只有红、蓝两种颜色(两个抽屉),所以至少有3条为同色,不妨设A1A2、A1A3、A1A4为红色。其次,再考虑△A2A3A4三边的颜色,若均为蓝色则结论成立(此三人互相不认识);否则,至少有一条边为红色,例如A2A3,则△A1A2A3的三边都为红色,结论也成立(此三人彼此都认识)。
例6已知某学者在五年期间内每月至少发表一篇文章,又知他每年至多发19篇,则可得结论:他必在某连续的几个月内恰好发文24篇,试证明之。
解设此人在5年内(60个月)每月发文数为a1,a2……a60,又设此数列前n项和为S1,S2,…,S60≤19×5=95。
如果他在某连续的几个月内恰发文24篇,则说明存在两个编号i和j,使得
Sj=Si+24(1≤i<j≤60)成立。
又S1+24,S2+24…,S60+24≤95+24=119共60个数,连同S1,S2…S60共120个数,将它们写在一起,即
1≤S1,S2…S60,S1+24…S60+24≤119
上式表明,在区间〔1,119〕中写了20个整数(元素),但〔1,119〕上只有119个不同的整数(设为抽屉)
上一页 [1] [2] [3] 下一页
|
