nbsp; 根据定理就能断定三条高线交于一点。
3:证明三条角平分线交于一点

证明:既然是角平分线,那必然少不了我们的角平分线定理,这里要用到的也正是他。因为Aa、Bb、Cc是其角平分线,根据角平分线定理,有下面的三个式子成立:
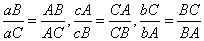
将三个式子左右相乘,约掉该约的,就得到:
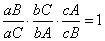
由此证明了三条角平分线交于一点。
我们至此应该可以明白为何三角形有那么多三线合一,原来他们都满足塞瓦定理!通过这两篇文章的讲述,我们的眼光就应该可以放宽了,更加明白藏在这些性质中间的统一思想。
文章来源:学夫子数学博客
上一页 [1] [2]
|
