昨天我们介绍的三角形的截线定理以及其逆定理,是有关三点共线的一个定理,利用他可以很漂亮滴证明许多有用的定理。今天我们利用截线定理来证明另一个重要的定理,那就是有关三角形里三线共点的问题。
定理:设过△ABC的顶点做相交于一点O的直线Aa,Bb,Cc,那么,这三条直线分别交边BC,CA,AB于三点a,b,c,满足关系:
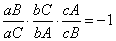
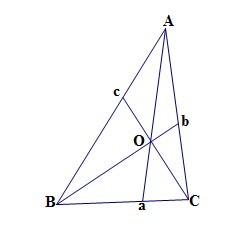
要注意的是,这里的线段都是有方向的,aB与aC反向,所以最终乘积等于-1,这里的负号就是这么来的,如果抛开这一点,你完全可以记忆成结果为1,但是最好习惯有方向的记法,在涉及到向量的时候会方便一点。
证明:△AaC被直线Bb所截,根据三角形的截线定理,有下面的式子成立:
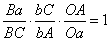
同理,△AaB被截线Cc所截,所以有:
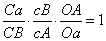
将上面两个式子两边相除,并约去OA/Oa,得到:
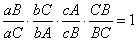
由于CB=-BC,就得到了结论中的定理。
如果你一下子不觉得这个定理有什么用的话,那么他的逆定理就是再熟悉不过了
逆定理(塞瓦(ceva)定理)
设在△ABC的各边上各取一点a,b,c。使得:
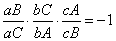
成立,则直线Aa,Bb,Cc共点。
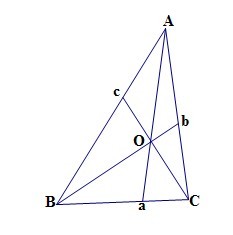
这个定理就是著名的三角形三线共点问题的解答了。我想大家都清楚,三角形三条高交于一点,三条中线高于一点,三条角平分线也交于一点。为什么这些线都交于一点?这些所有的性质之间是否有一个共同的表述?塞瓦定理就是最好的答案。
[1] [2] 下一页
