我们都知道勾股定理,古老的几何定理。也知道勾股数组,用来求解所有勾股数组的公式:m2-n2,2mn,m2+n2.我们也见过很多种推导方法,包括学夫子介绍的《勾股数的推导》。今天给大家介绍一种,并非学夫子原创,早已有之的结果,拿出来和大家分享。
设(a,b,c)为勾股数组,则:
a2+b2=c2.
两边同时除以c2,则变成:
(a/c)2+(b/c)2=1………………*
我们设a/c=cosα,b/c=sinα,并且0<α<90°。由于a,b,c都是整数,那么:
tg(α/2)=sinα/(1+cosα)一定是一个小于1的有理数,所以可以设tg(α/2)=m/n。根据万能公式
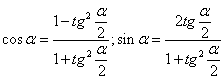
也就是有
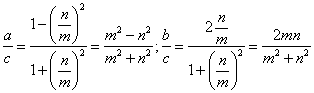
将式子带入*式,并化简就有:
(m2-n2)2+(2mn)2=(m2+n2)2
由此便得到了我们勾股数组表达式。这个方法没有多少难度,利用三角函数将a,b,c化成同一个量的表达式,不可谓不精巧。
文章来源:学夫子数学博客
|
