我承认,这题目取得有蛋疼,麻烦各位教我学学如何起名字,事情是这样的,彭翕成老师收到一朋友的来信,这位朋友看见一篇论文,因此迷惑不解。原信请进入彭翕成老师博客。这篇论文的内容大家也可以看见,我在这里就不贴出来,大体说说就行了。
我在不同的场合提到过”用向量法证明线面垂直“的内容,大体思路是:
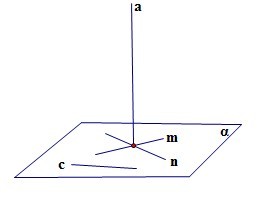
一个平面α和三条直线a、m、n,m和n在α上,m和n相交,a⊥m且a⊥n,证明a⊥α。
要证明a⊥α,只需要在α里任意取一直线c,只要证明a⊥c就行。根据平面向量理论,c向量可以用m向量和n向量表示(这里就直接用a和b表示向量了),于是我们设c=km+hn,其中k、h为常数。那么:
a·c=a·(km+hn)
=ka·m+ha·n
因为a⊥m,所以a·m=0,同理a·n=0,从而a·c=0,所以a⊥c。
这方法一直以来被奉为上宾,不只是学夫子,很多名师都提倡这方法。不过新疆的一位老师却提出质疑,因为在他看来,此方法犯了”循环论证“的错误。因为在这样一个证明过程里面,用到了”空间向量数量积的分配率“,这是关键的地方,因为我们在证明”空间向量数量积满足分配率“的问题上,又必须用到线面垂直的内容,因此犯了循环论证的错误,具体可以参考彭翕成老师博客里的配图,那里有论文全文。
首先我得感谢这位老师,我不得不承认,至始至终我都忽略了空间向量分配率的证明,在此对我是当头棒喝,深感惭愧。当一个人的思想观念受到质疑时,只有两条路可走:一是推翻质疑,一定要有足够的理由;二就是承认自己的错误和无知。对于这一个问题的解决办法,有这么一条路可以走,那就是绕过”线面垂直“。
1:一个比较”耍赖“的办法就是,我们用”证明线面垂直“的办法直接证明线线垂直(配图截取自原论文)
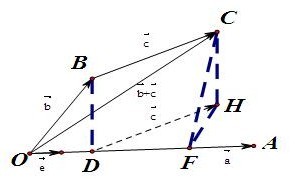
现在不是要证明OA⊥HF吗?我们这里就不直接用线面垂直的判定定理,我们直接用证明线面垂直的证明方法来证明OA⊥HF。想想线面垂直不就是证明平面里的任何一条直线都垂直于OA吗?那我们就直接用这方法证明OA⊥HF得了,很简单地绕过”线面垂直“这个话题。整体说来这个过程就是:用证明结论P的方法来证明另一个结论Q,反过来Q的证明可以大大简化P的证明。我觉得这并不算循环论证。
2:另外一个稍微有点好的方法就是,完全利用向量数量积的定义,跨过分配率,直接证明向量数量积的坐标表示
现在有a,b,c三向量,现在把他们的起点都移动到原点,并且设其坐标为a=(x1,y1,z1),b=(x2,y2,z2).
根据定义a·b=|a|·|b|·cosα。|a|=√x[1] [2] 下一页
|
