12+y12+z12,|b|=√x22+y22+z22,在a和b构成的三角形里,第三条边的长度为|c|=√(x1-x2)2+(y1-y2)2+(z1-z2)2,,利用余弦定理:
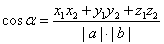
从而跳过了分配率直接得到数量积坐标公式:a·b=x1x2+y1y2+z1z2.这样我们就可以通过这个公式开始我们的证明了
现在是要证明:a·(b+c)=a·b+a·c
设a=(x1,y1,z1),b=(x2,y2,z2).c=(x3,y3,z3),b+c=(x2+x3,y2+y3,z2+z3).
左边=a·(b+c)=x1(x2+x3)+y1(y2+y3)+z1(z2+z3)
=x1x2+x1x3+y1y2+y1y3+z1z2+z1z3.
右边=a·b+a·c
=x1x2+y1y2+z1z2+x1x3+y1y3+z1z3.
左边=右边,从而分配率得证。
文章来源:学夫子数学博客
上一页 [1] [2]
|
