用发展联系的眼光看问题,你会有新的境界 |
|
|
| 来源:不详 更新时间:2011-12-23 12:17:20 |
|
|
|
|
很多东西,因为我们人为的分类,把他割得四分五裂,失去了他本来的美丽。有时候是为了研究问题的方便,也无可厚非,但是当我们的学识已经达到一种程度,可以将他重新联系起来的时候,我们就应该重新审视这些问题。
今天举得例子,就是等比数列
都知道,等比数列的求和公式
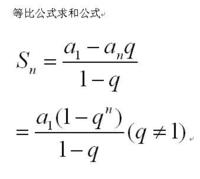
这是其中的一部分,还有一部分是:
Sn=na1(q=1)
等比数列的求和公式是要分情况的,即q=1和q≠1的情况。这样,最简单的等比数列——常数列就这样被分裂出来。让人感觉不舒服,而我们学习了极限,我们就拥有将他们合一起的能力。
我们看当q≠1的时候,当q趋于1时Sn的极限。
这个极限是很好求的,Sn的极限就是na1!(如果有人对求此极限还有问题,可以来问我,不喜欢数学的指点结果就行,呵呵)
答案就出来了,这两种情况并非一天一地,当q=1时的Sn只不过是q≠1时Sn的极限。那么等比数列的求和公式就可以用一个式子来表示:

当然,这比原来的还要麻烦,但是这显然让我们 重新思考了问题,使得这些分类的东西变成一个整体。
为何不呢?常数数列在数列中的作用就如数字中的0。如果我们将等比数列和等差数列比作数字中的正数和负数,那么常数列就相当于数字0.:0既不是正数也不是负数;而常数列既是等比数列也是等差数列!等差和等比这两个看起来毫无关系的概念,就是通过它联系起来。
我们反过来思考,难道就不能说q≠1的情况只是这个通式的一种特殊形式吗?我们竟然发现,通用的公式竟然只是一个无穷概念!
文章来源:学夫子数学博客
|
上一个数学: 备战数学学业考养成六习惯
下一个数学: 三角形三条重要的线的计算 |
|
|
|
|
|
|
