读彭翕成 |
|
|
| 来源:不详 更新时间:2012-1-3 20:03:09 |
|
|
|
|
今日读到彭翕成老师《为何0/0极限可以是任何值》一文。感触颇多,感触的不在于彭翕成老师对这个问题的解答水平,而在于作为一数学科普人的态度。用高等观点看初等数学,用初等观点讲述高数,这是学夫子一向崇尚的做法。彭翕成老师用一个图说明0/0的极限为何可以是任意值:
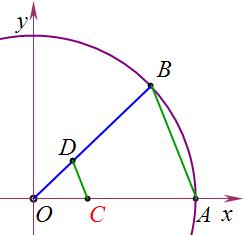
CD∥AB,当B点靠近A点,AB和CD的长度都趋于0,而AB/CD的值却是随着C点的位置改变而改变,比如C是中点的话,AB/CD=1/2,C点在三等分点的话,其值就为1/3,若C点与O点重合,其值就为正无穷……
这个图自然是精彩不过,只要知道中学的相似原理即可,学夫子喜欢凑热闹,就来个狗尾续貂:彭老师送出头几何法的貂,我就在后面续个代数法的狗尾。
下面几个分式,当x趋于零的时候,分别趋于不同的值,自然不过。
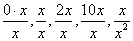
当x趋于零时,就是这位同学问的0/0情形,显然第一个极限值为0,第二个极限值为1.第三个为2,第四个为10,第四个化简为1/x,最终趋于无穷大。
为何0/0的极限值可以是任何值?我们首先要知道,当分子为非零数,分母趋于零时,这个值就是无穷大,这个在正切函数图像或者反比例函数图像里就可以看出一些门道。0/0的情形,其实就是分子分母都变成零的情形,同样是趋于0,却有着“快慢”之分,比如x2就比x趋近于0的“速度”要快。当分子趋近于零的速度比分母快的时候,分子占据优势,这时候整个分数的极限就是零,当分母的“速度”比分子快时,就是趋于无穷,当两者速度一样时,就是趋于一个常数。
文章来源:学夫子数学博客
|
上一个数学: 推荐一个超棒的数学网站——整数数列百科全书
下一个数学: 初中数学期末复习四原则 |
|
|
|
|
|
|
