这种问题比较常见,经常都会出现一个椭圆里的直角三角形,有的时候是让你计算,有的时候是让你解一些参数的范围。当椭圆上一点和两焦点形成直角三角形时,其实不外乎三种情况。这里讨论的都是F1F2为直角三角形斜边的情况
一种是曲线上有一个不在Y轴上的点能与两焦点构成直角三角形
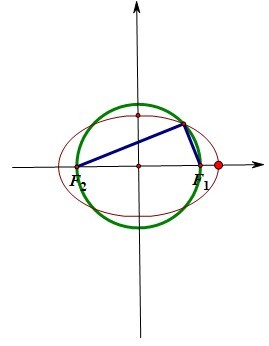
在这种情况下,一定还有其他点,而且一定有四个不同的点能与焦点形成直角三角形,因为如图所示,若我们以原点为圆心,C为半径做圆,那么满足条件的P点一定在圆上,而这个圆与椭圆的焦点若不在Y轴上的话,那么一定就有四个焦点,这从直观的角度就可以看出来。在这种情况下涉及到的不等式,就是圆的半径大于短轴,也就是c>b,所以如果让你求什么离心率的范围啊啥的,就可以利用不等关系,而若是相等关系嘛,那就是勾股定理了,在结合椭圆的定义,一般情况都能解答题目。
另一种情况就是当椭圆上有一个在Y轴上的点能与焦点形成直角三角形
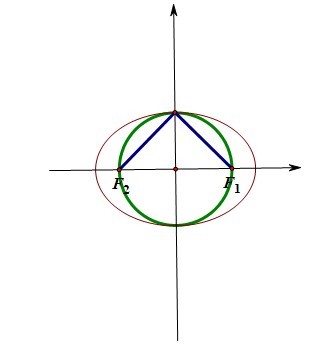
这种情况就很简单了,直观的角度就能看出来,此处最好的等量关系就是c=b,如果遇到这样的题目,什么勾股定理你都不用,c=b,解决一切问题。
最后一种情况,那就是椭圆上不存在这样的点,使得这个点和焦点无法形成直角三角形
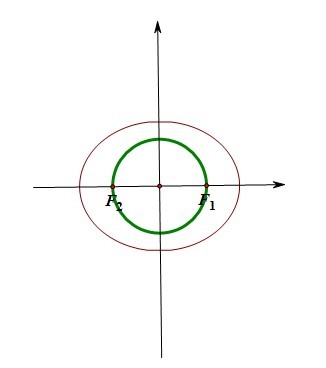
这种情况下的不等关系就是c<b.只要是涉及到什么求范围啊啥的就利用他。值得注意的是,有些时候题目当中是以一种委婉的方式告诉你的,比如下面这道题目:
例题:已知椭圆x2/a2+y2/b2=1,焦点为F1,F2,满足条件:
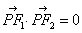
的点P都在椭圆内部,求椭圆离心率的取值范围
解:这个题目其实就是很委婉地告诉你,在椭圆上不存在使得PF1F2为直角三角形的点P,也就是我们上面的最后一种情况,显然满足c<b,利用他就可以求出离心率的范围:
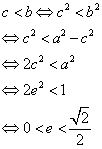
文章来源:学夫子数学博客
