我们都学过向量,都知道向量的一些运算律跟实数运算律一模一样,除了不满足结合律、消去率。正因为在实数运算的衬托下,这些运算律在我们看来是那么地自然,那么地想当然,或许我们早已忘记这些运算律的证明,就如同学夫子在“向量数量积分配率”这个问题上犯下的疏忽。关于分配率的相关信息,请参考文章《对“向量法证明线面垂直一法质疑”的回应》。今天我们来看看向量数乘中的分配率。
我们知道向量数乘的分配率成立:
λ(a+b)=λa+λb
其中a、b代表a、b向量。
不要看着这个分配率很简单,因为有了实数的对照。事实上他还有另外一个身份:向量数乘分配率实际上就是三角形相似原理的向量表示。也就是说,这其中其实包含了很重要的相似三角形理论。且看:
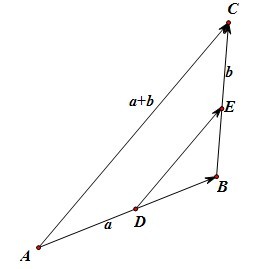
向量AB=向量a,BC=b,取向量DB=λa,BE=λb,DE=DB+BE=λa+λb,按照相似三角形的理论,此时△ABC∽DBE,所以向量DE=λAC=λ(a+b),所以向量数乘满足分配率律。因此我们说,向量数乘的分配率,实际上是相似三角形理论的向量刻画。平时我们没有注意的东西,还藏着很重要的理论呢!
文章来源:学夫子数学博客
|
