我们昨天借助复数工具,摸索出了向量的除法,完全不用管他对不对,也不管是不是早已有之。学夫子是站在中学生的角度,教会学生如何自己去发现书本没有但是又渴望知道的东西。所以高手些就不要拍砖了。我们其实可以看出,向量的除法依赖于复数的乘法运算,当我们摸索出向量的除法规则时,自然而然就应该想到,应该与其对应的有一种向量的乘法。
我们还是将平面向量和复数对应起来,因为:
(p+qi)(r+si)=(pr-qs)+(ps+qr)i
所以我们完全可以去定义向量的另外一种乘法,因为点乘和叉乘都用上了,我们就给自己摸索出的乘法叫做星乘吧!符号记做※。
(p,q)※(r,s)=(pr-qs,ps+qr)
利用我们上一篇文章一样的方法,可以得到这种乘法一些很有意思的性质:
1:向量星乘的模等于向量模的乘积
证明:记Z=a※b
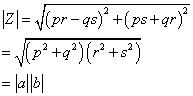
联系向量除法的性质:向量商的模等于向量模的商。可以看出这种定义下的向量乘法除法有着天然的数学之美。
2:向量星乘的倾斜角等于向量倾斜角的和
证明:记Z=a※b
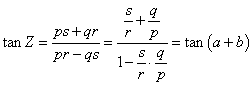
于是得证,联系起向量除法的性质:向量商的倾斜角等于向量倾斜角之差。便更加对这一定义充满好感了。
我们可以据此来定义向量的幂,也就是形如an。虽然在向量的数量积里面已经见过a2,但是这个更多只是为了方便,因为如果按照这个定义下去就比较麻烦:a2是一个数,a3是一个向量,a4又是一个数。如此便非常不爽,如果我们按照我们刚刚摸索出的星乘来定义向量的幂的话,一切便来的非常自然,而且有下面的性质:
|an|=|a|n.
<an>=n<a>
其中<a>表示向量a的倾斜角。
如果同学们按照上面的过程推导出了结论,恭喜你,你真的有了重大发现,因为这其实就是复数理论里非常重要的“棣莫弗公式”。相关内容可以参考百度,也可以参考学夫子的一篇文章《棣莫弗公式和n倍角公式》。
不过说来说去,这事还是有很大的麻烦,那就是这种规则只适合于平面向量,对于空间向量照这样子就没法弄。至于到底应该如何规定空间向量的乘除法?还需要各位同学进一步学习。
文章来源:学夫子数学博客
|
