学夫子用了两篇文章来谈这个问题,第一篇解决了一半,第二篇介绍了当xy=yx时的充要条件的证明。不过一个更主要的问题仍然没有被解决,那就是当x和y中,x>e,而y<e的情况,这个时候我们第一篇里的方法就失效。学夫子在写完《xy=yx的充要条件的证明》一文后,突然想到了可以利用其结论,来得到一种解决这个问题的可行办法。本文讨论的都是当x和y都大于1的时候。
xy和yx的大小比较
1:如果x和y均大于等于或者都小于等于e,则
A:当x>y≥e时,xy<yx;
B:当e≥x>y时,xy>yx.
2:倘若x和y分布于e的两边,我们设x>e,y<e
我们在《xy=yx的充要条件的证明》一文里已经提到
xy=yx,当且仅当存在实数t,使得:
y=(1+1/t)t,x=(1+1/t)t+1.其中x>y。
这个结论使得我产生了下面的想法,我们完全可以通过这一结论创造出下面的判断方法。这个方法基于这样一个事实:那就是函数f(t)=(1+1/t)t在t>0时是一个单值函数。
思考过程:假设x>y,先考虑xy>yx时会有什么结果
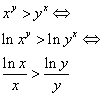 因为x>y,y<e,所以我们不妨令y=(1+1/t)t,x=(1+1/t)t(1+k),将之带入上式并化简后有:
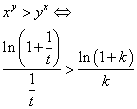
我们在昨天的文章里已经说过,函数y=ln(1+x)/x在(0,+∞)是单调递减函数,所以最终:
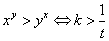
如果我们再结合函数f(t)=(1+1/t)t在(0,+∞)是单调递增的特性,就可以创造出下面的判断办法:思考过程结束
A:要判断xy和yx的大小,首先你要判断x和y的大小,这个不是问题吧! [1] [2] 下一页
|
