假设x>y
B:计算x/y,则k=x/y-1,计算
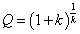
C:判断Q和y的大小,若y=Q,则xy=yx;若y>Q,则xy>yx;若y<Q,则xy<yx。
因为若是y>Q,那么也就是(1+1/t)t>(1+k)1/k,k>1/t,从而xy>yx.反之也成立。
这就是今天学夫子要给大家介绍的一种判断ab和ba大小关系的一种方法。我们最后以一个例题来结束今天的讨论,例题来源于彭翕成老师所提供的论文里的题目,原论文可以参考彭老师的文章。
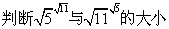
解:k=√11/√5-1=√2.2-1
Q=√2.21/(√2.2-1)>√5.
所以前者小于后者。经过伟大的计算器检验,这个结论正确。这后面有点麻烦的便是其计算Q了,往往很繁琐,不过我们可以采用估算的方法。这就是这个方法一个很大的缺点。所以我只能说这只是一个可行的方法,还谈不上完美。不过在x和y都是整数的时候,计算起来就比较快。学夫子只是把我的思路写下来,希望能引起各位同道共鸣。能找出一个更好的办法来解决这个问题。这个方法或许最大的优点就是将两个计算转化为一个计算。
写完这篇文章后,彭老师恰好发表了一篇关于nn+1和(n+1)n大小比较的文章,彭老师采用的是猜想归纳法。证明了当n≥3时,nn+1>(n+1)n,当我们有了本文的结论以后就可以很好滴理解这个结论了,其实就是我们的第一种情况。
上一页 [1] [2]
|
