昨天我们通过导数工具探讨了《xy和yx之间的大小关系》。在后面简单提到了一下当xy和yx相等的情况,我觉得有必要来介绍一下当他们相等时公式的证明和推导。为了能让大家看懂,我用了一种比较简单,也比较耍赖的办法来证明。说这方法耍赖,是因为原则上我是知道答案后制造的推导方法。本文讨论的都是x和y均大于零的情况。
先上结论:
xy=yx,当且仅当存在实数t,使得:
x=(1+1/t)t,y=(1+1/t)t+1.其中y>x。
证明:必要性
在昨天的文章里我们谈到,要让 xy=yx,其实只需要让lnx/x=lny/y,当然其中最简单的一种结果就是x=y,这个情况我们忽略,现在就考虑x≠y的时候,该文章里我们也谈到,函数f(x)=lnx/x只有一个极值点,换句话说,欲让lnx/x=lny/y,除了x=y以外,对于特定的x,也就只可能有一个符合条件的y值。这个很重要,因为这就告诉我们,若是x已经确定,那么y也就确定。
我们更知道,xy和yx之间的大小,是以e为分界线,当x和y同时大于e或者同时小于e时,他们不可能相等,所以唯一的情况就是当x和y分别处于e的两边,不妨设x<e。在这里就遇到关键点,我们需要创造出x的一个表达式,使得他恒小于e,这让我们想起e的定义,如果我们设x=(1+1/t)t,其中t>0,那么x<e,我们这样做是基于一个原则,那就是f(t)=(1+1/t)t可以取0到e之间的任何值。由于y>x,所以我们不妨设y=(1+1/t)t(1+k),其中k>0.带入相应的等式中有:
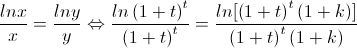
经过一系列化简后得到:(化简过程我就忽略啦!)
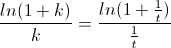
这个方程的一个解是k=1/t,而根据前面所说的结论,这个方程的解也只有这一个,否则将会出现不同的y值。这个结论还可以通过绘制函数图象的方式来证明。这样一来,y=(1+1/t)t(1+k)=(1+1/t)t+1.从而证明了我们的结论。
至于充分性方面就很简单了,你将两个式子带入,通过化简即可证明他们成立。所以最终,这个问题就算是解决:
xy=yx,当且仅当存在实数t,使得:
x=(1+1/t)t,y=(1+1/t)t+1.其中y>x。
问题到这里,似乎已经解决完,不过我们依然可以挖出一些好东西,通过x和y的表达式可以看见,如果让xy=yx,并且x和y都是整数的话,那么t就只能取1,也就[1] [2] 下一页
|
