作者:学夫子
等边三角形有一个众所周知的性质"三角形内一点到三边的距离之和为一常数k,k等于三角形一边的高。这不由得让我想起与之相似的,关于圆的“圆幂定理”。他们体现出一种公平性,只要你生活在圆的周围,不管你的地位如何,都有相同的性质。不过与正三角形不同的是,圆的这一性质可以推广到该平面内的任一点,但是正三角形的这一性质却只局限于三角形内的点,未免让人遗憾。其实正三角形的这一性质可以朝着不同方向进行推广的。
正三角形的这一性质可以通过面积法证明,就不必过多说了
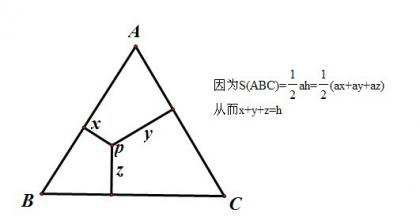
推广方向1:当P点在外面
在推广之前,有必要介绍几个概念,我不知道现在有没有类似的概念,但是我查了一些初等数学书并没有查到,于是自己编了几个。希望不要介意。
对于一个多边形,考虑该多边形的一边AB和该平面内的一点P。如果△PAB所表示的平面区域与多边形有交集(不包括边缘),那么则称P点在边AB内部,否则称点P在AB外部,如下图所示,P点在AB外部,在AC和BC内部;而Q点在边AB和AC外部,在边BC内部。
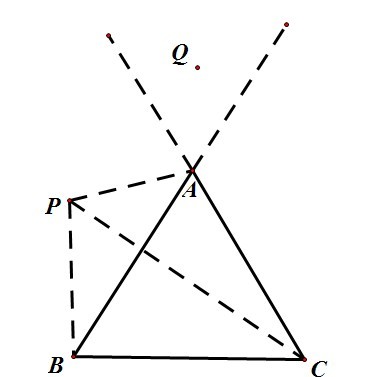
如果我们过P点做AB边的垂线,当P点在AB外部,我们成这条高为外高,否则称为内高,那么,关于正三角形的性质就可以进行下面的推广:
过P点向各边做高,所有内高之和减去外高之和为等于一常数k,k等于三角形一边的高。这个性质的证明可以用相同的方法证明。
推广方向2:正三角形变成正多边形
结论是显然的,证明方法也是显然的:正多边形内一点到正多边形各边的距离之和为一常数k,k=2s/a,s为正多边形面积,a为边长。很显然的,我们还可以将推广1的结论拿到正多边形。
推广方向3:平面变成空间
平面里面是通过面积法,空间里面就可以用体积法:正多面体内一点到各面的距离之和为一常数k。k=3V/S。V为正多面体体积,S为一个面的面积。同理可以推广到当P为正多面体外一点的时候。(来源:学夫子数学博客)
|
