作者:学夫子
不等式中的恒成立问题一直是不等式里常考的题目。因为新版教材已经将不等式证明的内容淡化,那么不等式的解法和应用自然就成为代替位置。今天学夫子就总结一下常见的恒成立问题及其解决办法。需要注意的是,还要能够判断以其他词汇隐含出的恒成立问题,比如“不等式的解集为R”,“不等式的解集为空集、不存在这样的解(其反面就是恒成立)”。
一:有关二次不等式的恒成立问题
这种问题只需要考虑两个方面——二次项系数和判别式。二次项系数分为大于零,小于零,等于零的情况。判别式的符号,一般情况下,判别式需要小于零。如果结合函数图像会更好。
例题:已知mx2+2x+3<0对于所有的x恒成立,求m的取值范围。
解:(1)当m=0,不满足条件
(2)当m≠0,必须要求m<0,并且Δ=4-12m<0
根据上述讨论即可。
二:两个未知数的恒成立问题
所根据的原理就两句话:若f(a)<g(x)对于所有的x恒成立,则只需要f(a)小于g(x)的最小值即可;若f(a)>g(x)对于所有的x恒成立,只需要f(a)大于f(x)的最大值即可.理解这个后,剩下的问题就是求f(x)的最值了.这就需要我们对常见函数的值域求法非常熟悉.
例题1:已知不等式|x+1|-|x-3|<a2-a对于所有的x恒成立,求a的取值范围
例题2:已知不等式|x+1|-|x-3|<a2-a对于所有的a恒成立,求x的取值范围
解:要注意这两个问题的不同.第一个只需要左边小于右边的最小值即可.第二个问题恰好相反,只需要右边大于左边的最大值即可.问题就只剩下求最值的问题了.对于二次函数的最值问题肯定不在话下,而对于绝对值的最值似乎有些同学就感觉比较麻烦了。对于这两种绝对值函数,你大可以总结出他们的各种性质,到时候可以快速得出答案
附图:形如|x-a|±|x-b|的性质(图像,最值,对称性)
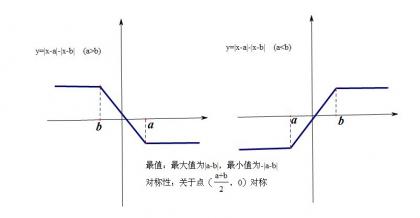
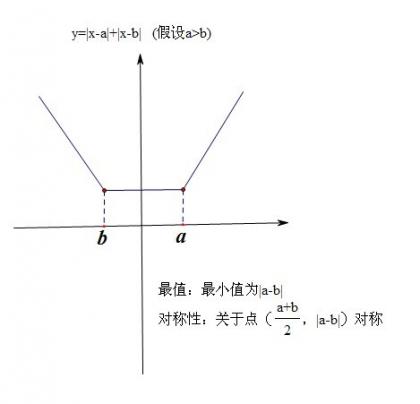
正如我们前面所说,有时候题目并没有明确告诉你这是恒成立问题,但是本质上就是,比如下面的例题:
例题:若不等式x+|2x-1|<a的解集为空集,则实数a的取值范围是________
解:"不等式x+|2x-1|<a的解集为空集"等价于"不等式x+|2x-1|≥a对于所有的x恒成立".只需求出左边的最小值即可,这可以借助函数图像.
例题:已知关于x的不等式|x-3|+|x-4|<a的解集为空集,求a的取值范围
同理可解,原命题等价于|x-3|+|x-4|≥a对于所有的x恒成立.(来源:学夫子数学博客)
