作者:学夫子
如果你注意到复数角度的运算法则,你便会发现他与对数的运算法则是如此的相似,这当然不可能是巧合。这样一个运算法则的好处是显而易见的,他将复杂的角度运算转变为简单的加减乘除,因为我们知道求反三角函数并非轻而易举之事,在涉及到反三角函数的一些题目,运用复数往往可以带来意想不到的效果。我们先来看看角度运算与对数运算之间的联系:
设复数Z的夹角为argz,则有下面的运算法则成立:
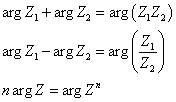
很明显,这和下面的对数运算法则简直就是如出一辙:
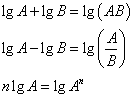
这里面到底有何关系使得他们的预算法则如此雷同?如果你注意到下面的式子成立,那么一切便是非常显然的事情:为了方便,我们只讨论角度不是π/2和-π/2的时候.

如此一来,分别在两边取对数就有:
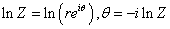
现在再回头看角度的运算法则,就能够理解他为什么和对数运算法则如此雷同的原因了.正是因为这些运算法则,使得在很多时候运用复数来求解三角函数题就显得非常简便,以几个例子说明:
例1:若arctanx+arctany+arctanz=π,则x+y+z=xyz
证明:设arctanx=arg(1+xi),则根据条件有:
arg(1+xi)+arg(1+yi)+arg(1+zi)=arg([(1+xi)(1+yi)(1+zi)]=π.
这说明复数(1+xi)(1+yi)(1+zi)的角度为π,也就是说其虚部为零,即:
x+y+z-xyz=0.得证.
例2:如图是三个大小相等的正方形,证明∠1+∠2+∠3=π/2.
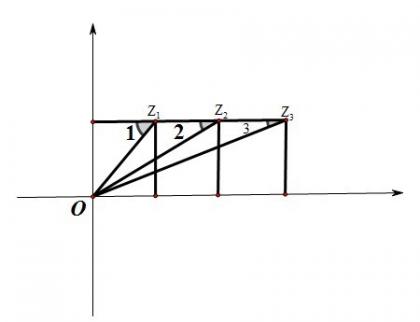
这是一道非常经典的题目了,有很多种证明方法,其中复数方法算是比较简洁的,我们建立复平面坐标系,正方形边长为1,则Z1=1+i,Z2=2+i,Z3=3+i.那么:
∠1+∠2+∠3=argZ1+argZ2+argZ3=arg(Z1×Z2×Z3)=arg[(1+i)(2+i)(3+i)]=arg(10i)=π/2.
当然类似的题目还有很多,在这里就不多说了.(来源:学夫子数学博客)
|
