作者:学夫子
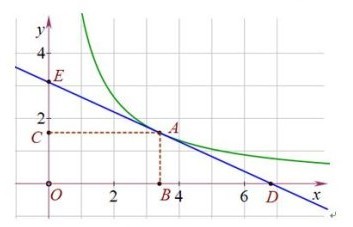
我们知道,对于反比例函数xy=k,过曲线上点A做两坐标轴的垂线,形成的矩形面积为一定值k,不过可能很少有人知道,过A点做曲线的切线,切线与坐标轴相交于E和D点,则三角形EOD的面积为一定值2k,具体证明过程请参见彭翕成老师博客,学夫子在这里就不废话了。我想说的就是这个结论本身。其实,此结论更有一般性的结果,我们知道,反比例函数的另一个身份是双曲线,关于他们之间的关系可以参见文章<双曲线与反比例函数>,正因为这个身份,其实对于一般的双曲线,这个结论也成立,即有:
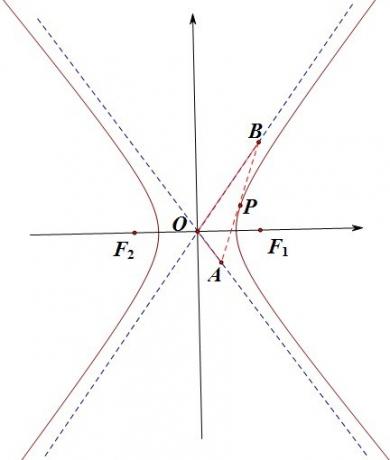
结论:过双曲线一点P做双曲线的切线,分别交两条渐近线于A和B两点,则△OAB的面积为一定值。
如果知道了这个结论,那么一开始的结论便是一种特殊情况。因为反比例函数图像就是旋转后的双曲线,并且两条坐标轴就是该双曲线的渐近线。具体可以参考《双曲线与反比例函数》一文,里面有详细介绍。
对于上面这个结论的证明,如果是运用纯粹的导数法的话,计算量就比较大了,但是最终还是能证明的,一个好一点的方法就是变换法。这要用到一些结论,比如:
将三角形三点坐标按下面方式进行压缩变换:
x‘=x
y’=ky
比如将坐标(1,2)变换成(1,4),这里的k就是2。按此方式变换以后,得到的新三角形的面积S'为原三角形面积S的k倍,证明他要用到行列式知识,如果三角形三点坐标为A(x1,y1),B(x2,y2),C(x3,y3),则三角形ABC的面积为:
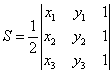
然后利用行列式的基本性质即可证明之,在这里就忽略了.这样一来,我们就可以先将一般的双曲线变换到等轴双曲线,这样得到的新三角形的面积就变成原来的K倍(这里的k=a/b),然后将等轴双曲线逆时针旋转45°就得到xy=c曲线,注意到旋转并不影响三角形面积.这样上面的两步都不影响三角形OAB的面积为定值这一性质,只要能证明xy=c也满足此性质,则就可以证明对于一般的双曲线结论也成立。
学夫子在这里就有点问题求助:证明这个结论是否有更简洁,适合中学生的方法?希望能和大家一起交流,毕竟现有的证明方法对于中学生来说比较高端了。(来源:学夫子数学博客)
|
