作者:学夫子
因为出现多道非常类似的题目,所以学夫子觉得有必要总结一下他的解决办法,希望对大家有所帮助。涉及到向量的最值问题,特别是求某一个向量的模的最值,一般情况下我们有几种解决办法:涉及到坐标的采用坐标法,没有坐标的考虑平方后将其激活为向量运算,而如果这两种都行不通,那我们就应该尝试着用几何方法。
为了方便,下面的字母默认代表向量,不是向量的参数我家绝对值符号
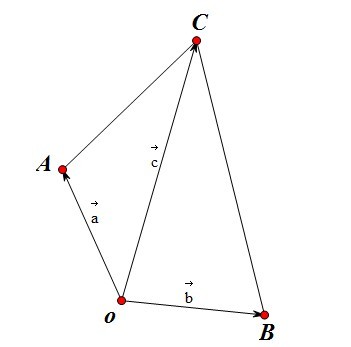
例1:(2011全国)设向量a,b,c满足|a|=|b|=1,a·b=-1/2,<a-c,b-c>=60°,则|c|的最大值等于()
解:此题没有坐标,所以抛弃坐标法(其实坐标法也可以,因为根据他的条件很容易设置坐标),我们对|c|平方,但是也无法激活,因为我们无法把向量c表示为a和b的表达式,也就无法用条件,这是我们就可以考虑用几何法:
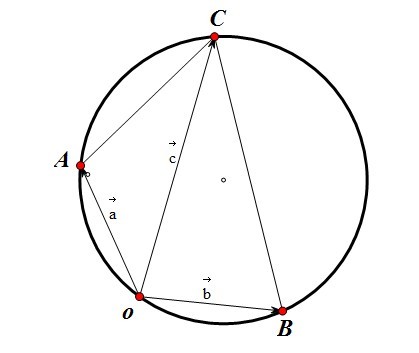
如左图所示,a与b之间的夹角为120°,∠ACB=60°,所以,AOBC四点一定在一个圆上,如右图所示。现在要求|c|的最大值,就是求右图中那一条弦的最大值了,结果非常显然,最大值就是该圆的直径。
与之完全相同的题目便是08年浙江的一道高考题:
例2:已知向量a、b是平面内两个互相垂直的单位向量,若向量c满足(a-c)·(b-c)=0,则|c|的最大值为()
解决办法就交给各位自己了,与例1一模一样的方法。答案为根号2.
在最后,很多学生反映对向量的减法有点混淆。在这里有两个方法可以解决这个问题,一种就是将减法看成加法,减去一个向量就是加上其相反向量。另一个方法就是结合向量的坐标运算:向量的坐标等于终点坐标减去起点坐标,类比到向量的减法也是如下图中:m=a-c,m是终点减起点,a的终点为m终点,c的终点就是m的起点,所以m=CA。很多概念类比记忆会有很多帮助的。(来源:学夫子数学博客)