作者:学夫子
两圆周的正交:
两圆相交,若两圆周在交点处的切线的夹角为直角,则说两圆周相交成直角。如下图所示的圆O与圆O'就相交成直角或正交。
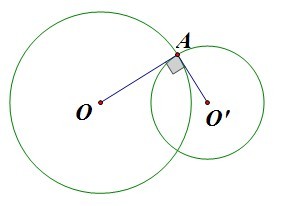
我们关心的是,根据简单的切割线定理知道:O'对于圆O的幂是一个定值,这个定值只随着圆O'的大小而变。同理O对于圆O'的幂也是一定值。如果我们同等幂定理一样,考虑两个圆,那么我们就有下面的性质:
两圆周的根轴,是和此两圆周正交的圆周的圆心的轨迹。
这个很好证明,因为这样的圆心对于已知两圆有相等的幂。根据昨天的等幂定理即可得上面的性质。
认识了两圆的根轴,这个根轴就应该用来代替我们常说的公共弦,因为公共弦这个概念有很大的局限性:只有相交圆才具有公共弦,但是任何两个圆(除了同心圆)都有根轴。(来源:学夫子数学博客)
|
