初二数学期末备考攻略 |
|
|
| 来源:不详 更新时间:2012-6-15 12:24:43 |
|
|
|
|
考察,此类问题同学们也可以多做一些相关练习提高水平。
二、几何
几何部分重点分为三部分:中点问题、梯形构造辅助线、三大变换。
中点问题:
说明:当考试题目中出现了“中点”两个字的时候,同学们可以构造:中位线、倍长中线、斜边中线、三线合一这四种辅助线。当然如果题目非常难,很有可能同时构造这四种辅助线当中的两种甚至三种。
(去年的西城区、朝阳区统考都出现了中点问题,包括刚刚结束的17个区县的一模考试试卷中有12个区县都出现了中点问题,所以今年出现的可能性也非常大。同学们一定要多注意此类题型)
梯形构造辅助线的8种方法:
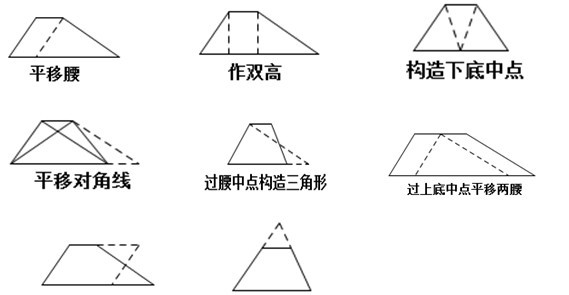
说明:
平移一腰:当梯形的两个底角互余时,可以选择平移一腰,把一个梯形分割成一个平行四边形和一个直角三角形。
做双高:当梯形的底角出现特殊角时,可以构造高。
构造底边中点:目的构造三个全等等边三角形。
平移对角线:当已知出现“上底加下底”,并且题目中出现对角线时,可选择平移对角线。
取一腰中点:当已知出现“上底加下底”,并且题目中无对角线时,可取一腰中点。
过上底中点平移两腰:目的构造直角三角形。
过腰中点:可构造平行四边形
延长两腰:构造三角形(可能出现三线合一)
三大变换:
说明:三大变换是初中几何的精华所在,在初三的上学期期末,一模考试以及中考中都占有很重要的位置,初二的期末考试开始逐渐向初三过度,同学们在平常的联系中也会感觉到运用三大变换进行解题的方便,故而在此次期末考试复习中,一定要尽快熟悉起三大变换。
1、平移:平移模型有三种。
a)“相等线段相交模型”我们需要通过平移将两条线段构造成共顶点的图形,进而构造出三角形去凸显条件。
b)“相等线段不想交模型”此类模型的辅助线构造方法与第一种类似,都是通过平移线段使得两条线段共顶点,进而解决问题。实际上平移线段就是构造平行四边形,而我们初二的学习重点就是平行四边形,所以在复习过程中有关平移的题目一定不能马马虎虎。
c)当题当中出现了两条相等的线段并且相等线段共线或平行时,可选择平移。
2、旋转:一般来说旋转的模型都有着“共顶点的等长线短”这个特点,当然有些很难的题目没有这种特点那么我们则需要去将此特点构造出来,例如费马点的证明。当同学们做了很多有关旋转的题目之后可以总结出来哪些题目比较“像”能有旋转做出来的题,要多总结一些模型,例如半角模型,构造等边三角形的模型等等。下面说一些关键点给同学们参考。
a)确定有没有“共顶点等长线短”,没有则需要构造。
b)确定要旋转谁。一般来说旋转对象为等长线短其中一条所在的三角形。
c)确定转多少度。这个度数基本上由等长线短的夹角决定。
d)确定旋转之后的等量关系以及是否需要添加其他辅助线以构成特殊图形。
3、轴对称:轴对称是我们初二上学期的学习内容,期末也会考察希望同学们不要遗忘掉这部分知识。下面给出几种常见考虑要用或作轴对称的基本图形。
a)线段或角度存在2倍关系的,可考虑对称。
b)有互余、互补关系的图形,可考虑对称。
c)角度和或差存在特殊角度的,可考虑对称。
d)路径最短问题,基本上运用轴对称,将分散的线段集中到两点之间,从而运用两点之间线段最短,来实现最短路径的求解。所以最短上一页 [1] [2] [3] 下一页
|
上一个数学: 初一数学三周突破期末考试
下一个数学: 棣莫弗公式与n倍角公式 |
|
|
|
|
