作者:学夫子
初中学过两倍角公式,很多参考书也介绍过三倍角公式,我们自然而然就会想到n倍角公式。我想好奇心强的同学肯定干过这样的事:用和的公式将四倍五倍展开,然后观察他们的规律,不过都是无功而返。这个问题的解决,得要归功于著名的棣莫弗公式,涉及到复数的内容,不过你只要知道复数符号“i”是什么意思就足够了:
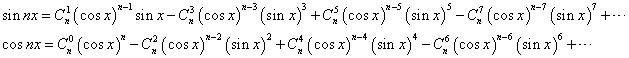
这个公式的作用可不单单是拿来进行复数运算,若我们对右边用二项式定理展开后,对比左右两边的实部和虚部,将得到n倍角公式:
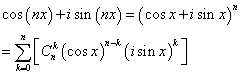
且看下面一行,当k取偶数的时候,这一项就是实数;当k取奇数的时候,这一项就是虚数。到最后所有的实数就构成结果的实部,所有的虚数项就构成结果的虚部。根据复数相等的规则,左右两边的虚部和实部应该相等,那么就有:
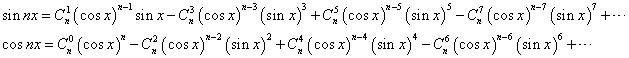
这后面就一直写,直到写不下去为止
这个就是n倍角公式,维基百科里有常用的n倍角公式,大家可以参考参考。其实就算是要推导的话也不会太难,只要知道二项式定理就不在话下。
大家都知道,学夫子的原则是,不会随便抄点网上的东西就算一篇文章。这里也是一样,写这篇文章只是一个预热,担心有朋友不知晓这一公式,更重要的地方时,我们将在下一篇文章给出一个问题的证明,那就是我在《将圆N等份,漂亮至极的结论》一文里提到的一个性质:
将一个单位圆N等分,取其中一个N等分点,则这个点到其他N-1个点之间的距离乘积等于N。
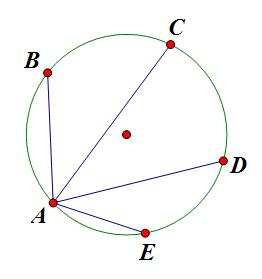
比如下图所示,A,B,C,D,E为单位圆的五等分点,那么过A点做B,C,D,E三点的连线。那么有AB×AC×AD×AE=5
来源:学夫子数学博客
|
