作者:佚名
新课程理念要求数学教学是数学活动的教学,是师生之间,学生之间交往互动与共同发展的过程。数学教学应从学生实际出发,创设有助于学生自主学习的问题情境,引导学生通过实践、思考、探索、交流,获取知识,形成技能,发展思维,学会学习,促使学生在教师指导下生动活泼地、主动地、富有个性地学习。我认为,数学教学应注意这样几个问题:
一、创设合理的情境
新的教育理念认为:在教学过程中,学生应自始至终处于主体地位,教师是参与者,合作者和引导者,教师要相信学生是愿意学习的,也是能够学好的。因此,教师要结合具体的教学内容采用“问题情境--建立模型--解释应用与拓展”的模式展开,让学生经历知识的形成与应用的过程,从而更好地理解数学知识的意义,掌握必要的基础知识与基本技能,发展应用数学知识的意识与能力,增强学好数学的愿望和信心。
例如:《直角坐标系的建立》一课,可这样进行提问:进入教室你们怎么找到座位的?学生回答:看同座、前座或者后座。再问:假如你是第一个到教室的呢?学生答:找第二排第二张桌。然后教师和学生共同把班级的座位用图形表示出来。请同学到黑板上圈点出自己的座位,由此进一步得到直角坐标系。
这样引课,教师首先激活了学生头脑中的生活经验,让学生在原有生活经验上经历数学知识的形成过程,从而达到对新知识的建构。
从此案例可以看出,通过教师创设情境,不断启发引导学生积极活动,学生始终保持着发现、创造的兴趣,比较完整深刻的在原有生活经验的基础上建构“直角坐标系”这一新知识。
二、合理强化训练
执行新的课程标准,培养学生多创新意识和创新能力,就要通过强调问题的新颖性、综合性,开发新的题型来达到目的。
有观点认为:传统教学中的基础训练是一种浪费,是对学生创造力的扼杀。实际上我们应该认识到题海战术,无限制强化训练是错误的,但必要的、合理的基本训练仍然是学习数学过程中所必须的。美国心理学家吉尔福特认为:创造性思维具有流畅性,就是在一般性的思维定式上产生的。熟能生巧,“熟”是前提,是必经阶段,学生在构建自己的实践活动进行思考,发现规律,形成概念和技能。这项训练达不到一定的量,其概念和技能的形成就不牢固,因而应引导学生多角度、换方位地思考,形成更丰富的技能,这样才能更深刻地认识新旧知识的联系,产生新的思维火花,使学生的知识升华到“理解”,并达到“融会贯通”的境界。
(一)加强基础性训练
在课堂教学中,应加强基础题训练,以巩固知识为主,突出与课本同步或将课本习题加以改选,这样对学生的思维拓展大有益处。
例如:已知:如图梯形ABCD中,AB//CD,四边形ADBE是平行四边形,AB的延长线交EC于点F,求证:EF=FC
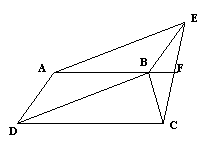
这是一道几何证明题,解法有多种。课堂上可以引导学生充分展开思维空间,探索多种引辅助线方法并给出不同的证明方法。通过一题多解的训练,达到培养学生发散思维的目的。
(二)加强图形训练
近年来,随着素质教育的不断升华,各地中考试题越来越重视考查学生的能力,关于图形问题已屡见不鲜。
例如:在学完了圆后,我让学生用一个三角形、一个矩形、一个圆设计一个轴对称图形并简要说明自己的创意(见下图)
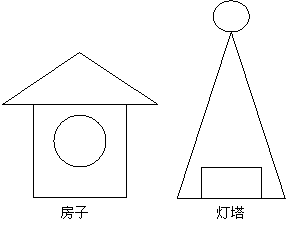
这是一道典型的图形组合设计问题。这类问题在实践中碰到很多。如:学校报刊设计中要求用某种几何图形为元素设计花边或图案。
所以,教师在教学中应当加强图形发散思维训练,把学生的发散思维向
[1] [2] 下一页
