学生在几何解题中的思维误区与中考复习

作者：佚名
　　
　　一、初中学生在逻辑推理中的思维误区
　　
　　学生的几何学习是以认识和发展平面几何知识为目的的一种思维活动，在这个过程中，学生将思维建立在几何概念和定理的基础上进行逻辑推理，然而推理的过程并不是一帆风顺的，学生解题过程中会暴露出思维上的误区，严重影响学生逻辑思维能力的健康发展．几何的推理论证要求一环扣一环，步步有据．但某些学生在进行几何证明时，由于逻辑思维往往不够缜密，致使他们的推理过程漏洞百出，归纳起来他们在进行逻辑推理的过程中，经常会出现以下几种思维上的误区．
　　
　　（一）移花接木
　　
　　所谓“移花接木”指的是推导出的结论与条件不相符，它是根据学生的需要生拉硬拽得出的结论，这种错误常常出现在全等三角形证明的过程中．这种错误不是学生的有意行为，而是一种无意行为，是他们没有意识到自己在思维上的一个误区．
　　
　　案例一、如图（1），已知在矩形ABCD中，AC与BD相交于点O，
　　
　　BE⊥AC于E，CF⊥BD于F．
　　

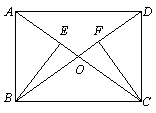
　　图（1）
　　
　　求证：BE=CF．
　　
　　有个学生的解答是：在矩形ABCD中，AB=DC．∵AC与BD是矩形ABCD的对角线，∴OA=OC，OB=OD．∴△AOB≌△COD．∴∠BAO=∠CDO．又∵BE⊥AC于E，CF⊥BD于F，∴∠BEA=∠CFD．
　　
　　在△ABE与△DCF中，∵∠BAO=∠CDO，∠BEA=∠CFD，AB=DC，∴△ABE≌△DCF．∴BE=CF．
　　
　　他在得到△AOB≌△COD后，误认为A点与D点对应，B点与C点对应，从而得到∠BAO=∠CDO，在不知不觉中实行了移花接木，在他的思维当中，他认为∠BAO=∠CDO是很自然、正确的，却没有认真思考这两个角是否是对应角．笔者认为出现这种错误的原因固然与他的基础知识不扎实有关，同时也与他的嘻嘻哈哈、不注重细节的性格有关．
　　
　　（二）无中生有
　　
　　“无中生有”指的是学生在答题的过程中，常常根据答题的需要，自己杜撰定理或条件．有些学生将看起来成立的但未经证明的结论或者某些定理的逆命题理所当然地认为是定理，而不假思索地应用到证明当中，有时也会根据图形的形状以及自己的需要杜撰条件．
　　
　　案例二、如图（2），在四边形ABCD中，AB∥CD，AC平分∠BAD，CE∥AD交AB于E，求证：四边形AECD是菱形．
　　
　　某些学生的证明过程是：连结ED交AC于点F，
　　

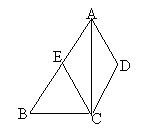
　　图（2）
　　
　　∵AB∥CD，CE∥AD，∴四边形ADCE是平行四边形，∴AC与ED互相平分，∴AF为DE的中线，又∵AC为∠BAD的平分线，∴△ADE是等腰三角形，∴AD=AE，∴□ADCE是菱形．
　　
　　证明过程中，他们理所当然地认为“等腰三角形的三线合一”会有一个逆定理，即：如果三角形中一个角的角平分线是对边的中线，则这个三角形是等腰三角形．基于这个考虑，她认为AF既是ED的中线又是顶角的平分线，所以△ADE是等腰三角形，在这里，这些同学不由自主地犯了杜撰定理的错误．
　　
　　（三）望“图”生义
　　
　　望“图”生义就是学生根据图形主观认定某个数学对象的存在，主要表现在习题的已知条件中并不存在的数学对象，而在图形中看起来象存在这种数学对象，而证明过程中恰好又可以使用，于是就顺理成章地被学生拿过来作为条件或结论加以使用．
　　
　　案例三、如图（3），已知正方形ABCD在直线MN的上方，BC在直线MN上，E是BC上的一点，以AE为边在直线MN的上方作正方形AEFG，连接GD，求证：△ADG≌△ABE．
　　

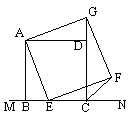[1] [2] [3] [4] [5] [6] 下一页