学生在几何解题中的思维误区与中考复习

）就不会被遗漏．
　　
　　从这里我们可以看出，学生头脑中分类讨论概念的形成不是一蹴而就的，因此在教学中，我们应当逐步给学生渗透分类讨论的意识，在渗透分类讨论思想的过程中，首要的是分类．教师要培养学生分类的意识，然后才能引导学生在分类的基础上进行讨论．在讨论中要坚持互斥、不漏、最简的原则，具体就是：（1）分类中的每一部分是相互独立的；（2）一次分类按一个标准；（3）分类讨论应逐级进行．
　　
　　（二）不能有效地借助类比思维方法
　　
　　类比思维是根据两个对象在一系列属性上相同或相似，由其中一个对象具有某种属性推测出另一个对象也具有这种属性的思维方法[3]．在数学上，它是一种非常重要的思想方法．很多探索题的解答如果能借助类比思维方法，就能起到触类旁通的作用．
　　
　　由于类比思维对学生的要求比较高，不少学生面对这种习题会选择放弃，也有些学生会跃跃欲试，但由于不能有效地借助类比思维的方法进行分析，往往会功亏一篑．
　　
　　案例六、邹骏程同学的思维比较活跃，喜欢挑战一些有难度的试题，但由于他自制力比较差，控制不住自己思维的信马由缰，在挑战难题时，经常会因为思维上的偏差、并且不善于借助类比思维的方法而前功尽弃．
　　
　　例7、如图（9），在△ABC中，D、E分别是AB、AC的中点，F、G分别是DB、EC的中点．
　　
　　（1）易证：△AFG∽△ABC，其相似比为：；
　　
　　（2）若AB=AC，将△ADE绕A点顺时针方向旋转到如图（10）的位置，判断△AFG的形状，并证明！
　　
　　（3）若AB≠AC，将△ADE绕A点顺时针方向旋转到如图（11）的位置，△AFG与△ABC有什么关系？说明理由！
　　

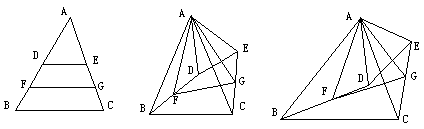
　　图（9）图（10）图（11）
　　
　　他在顺利解答出前两问之后，在解答第（3）问时卡壳了，他也试图类比第（2）问的解法来解决第（3）问，但在第（2）问中，由于AB=AC，AD=AE可以证明△ABD≌△ACE，从而得到AF=AG．而第（3）问显然要复杂得多，由于AB≠AC，因此AD≠AE，因而不可能得到△ABD与△ACE全等．他只想到用类比的方法证明全等，却没有想到相似三角形判定定理其实是类比全等三角形的判定定理得到的，此题也可以类比第（2）问中全等的证明，得到第（3）问△ABD与△ACE相似，证明方法也同样可以类比，第（2）问是用SAS证明△ABD≌△ACE，第（3）问可用“两边对应成比例夹角相等”类比证明△ABD∽△ACE．
　　
　　类比思维的教学应从简单的类比入手，如：首先从结论与证明过程可以完全类比得出的习题着手，然后逐步过渡到结论可以完全类比得出，但证明过程有所差异，最后过渡到结论与证明过程可以部分类比得出，但差异逐步加大，只有在完成了一定量的类比思维练习以后，学生才会逐渐掌握这种类比思维的方法，摸到其中的脉络，提高解题能力，使自己的思维能力更上一个台阶．
　　
　　三、中考复习
　　
　　由于学生思维不可能是统一的，他们对同一道证明题给出的证法是多种多样的，其中不乏错误的做法，但这些错误是真实美丽的，可遇而不可求的，这就要求我们教师及

上一页 [1] [2] [3] [4] [5] [6] 下一页