作者:佚名
提要笔者设计了一个数学实验──由学生利用Ti-92图形计算器作二次函数图象,通过观察、总结在给定的闭区间上,函数的单调性与函数取最值时自变量的取值的关系,寻找二次函数在闭区间上的最值问题的解决方法.由此攻破了教学中的一个重点、也是难点的内容,在此基础上探究另一些函数在闭区间上的最值问题的解决方法.同时看到现代教育技术手段的应用,为打破传统的教学模式(教师讲学生听)开辟了宽敞的道路.
主题词Ti-92图形计算器作函数图象单调性
一、实验背景:
高一学生在初中已学过二次函数,知道二次函数在x可取任意实数时在顶点处取得最大值或最小值,但定义域是闭区间时,二次函数在顶点处还取得最大值或最小值吗?所以笔者设计了一个实验,利用Ti-92图形计算器作函数图象,寻找二次函数在闭区间上的最值问题的解决方法.
二、实验目的:
通过观察函数图象的单调性与最值点的关系,寻找二次函数在闭区间上的最值问题的解决方法;在此基础上探究另一些函数在闭区间上的最值问题的解决方法.
三、实验工具:Ti-92图形计算器
四、实验预习题:(1)试求函数y=2x2-4x-1的最值.(配方法)
(2)试求函数y=x+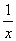 及y=x- 及y=x-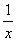 的最值.(判别式法) 的最值.(判别式法)
五、实验步骤:
(一)先利用Ti-92图形计算器作出系数为整数的二次函数,y=2x2-4x-1给定区间x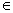 [-1,1/2]、[2,3]、[-1,2],分别通过F5中Minimum,Maximum计算出结果.观察函数图象的单调性与图中所示的最值点的位置的关系. [-1,1/2]、[2,3]、[-1,2],分别通过F5中Minimum,Maximum计算出结果.观察函数图象的单调性与图中所示的最值点的位置的关系.
(二)再改变二次函数,如y=2x2-4x-1及给定闭区间,x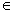 [-3,-2],[-1,1],[-2,1](闭区间要求分别在对称轴左、右侧及相应开区间包括对称轴),重复步骤(1). [-3,-2],[-1,1],[-2,1](闭区间要求分别在对称轴左、右侧及相应开区间包括对称轴),重复步骤(1).
(三)自行重新设置新函数,(二次函数的系数可为分数且二次项系数正、负均应有),重复步骤(1).猜想解决方法.
(四)实验现象记录:
1、在下面绘制出函数的图象.
函数y=2x2-4x-1,x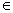 [-1,1/2]的图象 [-1,1/2]的图象
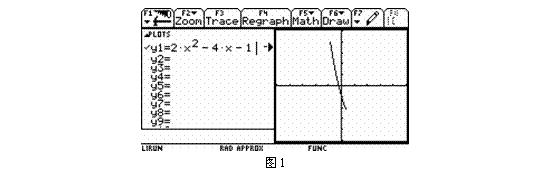
函数y=2x2-4x-1,x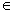 [2,3]的图象 [2,3]的图象
[1] [2] [3] [4] 下一页
|
