函数y=2x2-4x-1,x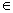 [-1,2]的图象 [-1,2]的图象
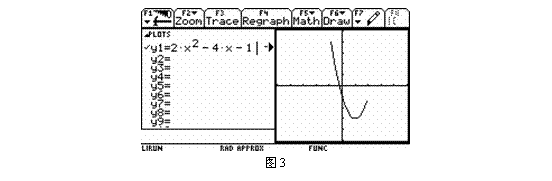
2、完成下表:分别记录函数图象的单调区间与图中所示的最值点的位置(x的取值).
二次函数
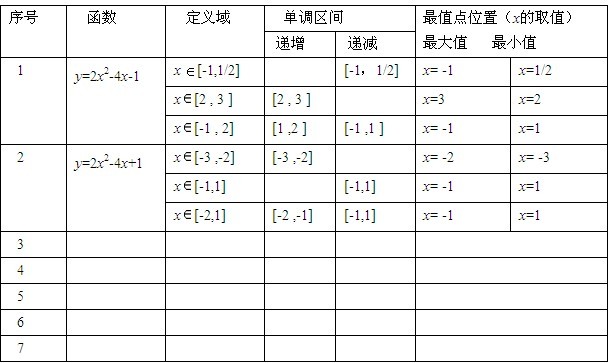
(上表中空白部分由学生自行设计填写)
六、实验结论:
(一)通过对以上函数的观察分析,你认为二次函数在闭区间上的最值问题有何规律?
(一个二次函数在闭区间上必有最大值和最小值.解决二次函数在闭区间上的最值问题.可通过闭区间的端点的函数值与顶点的函数值比较大小得出.当定义域分别在对称轴左、右侧,或闭区间的一个端点在对称轴上时,闭区间的端点的函数值为最大或最小值;当顶点的横坐标属于闭区间去掉两端点得到的开区间时,二次函数在顶点及距离顶点较远的闭区间的一个端点处的函数值为最大或最小值.)
(二)数学证明(利用函数图象的单调性可证.)
设函数f(x)=ax2+bx+c(a>0),x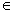 [m,n]则对称轴为x=- [m,n]则对称轴为x=-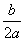 ,最值分情况 ,最值分情况
讨论:
[1]当m≥-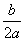 时,对称轴在区间左侧,f(x)在[m,n]上递增,则f(x)的最大值为f(n),最小值为f(m); 时,对称轴在区间左侧,f(x)在[m,n]上递增,则f(x)的最大值为f(n),最小值为f(m);
[2]当n≤-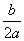 时,对称轴在区间右侧,f(x)在[m,n]上递减,,则f(x)的最大值为f(m),最小值为f(n); 时,对称轴在区间右侧,f(x)在[m,n]上递减,,则f(x)的最大值为f(m),最小值为f(n);
[3]当-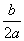 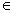 (m,n)时,则f(x)的最小值为f(- (m,n)时,则f(x)的最小值为f(-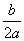 );在[m,- );在[m,-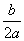 ]上函数f(x)递减,则f(x)的最大值为f(m),在[- ]上函数f(x)递减,则f(x)的最大值为f(m),在[-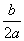 ,n]上函数f(x)递增,则f ,n]上函数f(x)递增,则f
上一页 [1] [2] [3] [4] 下一页
|
