(x)的最大值为f(n),比较f(m)与f(n)的大小即得.
七、拓展:
1、某蔬菜基地种植西红柿,由历年市场行情得知,从二月一日起的200天内,西红柿市场售价与上市时间的函数关系式为:f(t)=300-t:西红柿的种植成本与上市时间的函数关系式为:g(t)=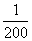 (t-150)2+100,认定市场售价减去种植成本为纯收益,问何时上市的西红柿纯收益最大?(2000年全国高考题)(转化为二次函数在闭区间上的最值问题) (t-150)2+100,认定市场售价减去种植成本为纯收益,问何时上市的西红柿纯收益最大?(2000年全国高考题)(转化为二次函数在闭区间上的最值问题)
2、求以下函数在给定区间的最值.
(1)若函数y=x2+x+a在[-1,2]上的最大值与最小值之和为6,则a=----.
(2)求函数y=-x2+tx-1(t>0),x[-1,2]的最值.(与实验结论的数学证明方法相同)
(3)求函数y=-x2-2x-1,x[t,t+1]的最小值g(t).
(分析:这里函数解析式已定,但是在一个含有参数的闭区间上考察最小值,就要结合区间与对称轴的相对位置进行定位讨论.)
解:f(x)=-x2-2x-1对称轴x=1
当x=1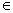 [t,t+1]时,即0≤t≤1时,g(t)=-2; [t,t+1]时,即0≤t≤1时,g(t)=-2;
当x=1<t时,对称轴在区间左侧,f(x)在[t,t+1]上递增,g(t)=f(t)=t2-2t-1
当x=1>t+1即t<0时,对称轴在区间右侧,f(x)在[t,t+1]递减,g(t)=f(t+1)=t2-2.
g(t)=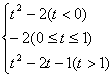
3、其它函数是否也可以利用函数图象的单调性解决在闭区间上的最值问题?如:
(1)y=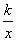 (k (k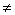 0),x 0),x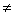 [2,4] [2,4]
(2)y=k|x|(k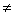 0),x 0),x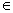 [-11] [-11]
(3)y=x+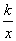 (k>0),x (k>0),x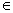 [ [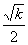 上一页 [1] [2] [3] [4] 下一页
|
