作者:佚名
●计名释义
比起“芝麻”来,“西瓜”则不是一个“点”,而一个球.因为它能够“滚”,所以靠“滚到成功”.球能不断地变换碰撞面,在滚动中能选出有效的“触面”.
数学命题是二维的.一是知识内容,二是思想方法.基本的数学思想并不多,只有五种:①函数方程思想,②数形结合思想,③划分讨论思想,④等价交换思想,⑤特殊一般思想.数学破题,不妨将这五种思想“滚动”一遍,总有一种思想方法能与题目对上号.
●典例示范
[题1](2006年赣卷第5题)
对于R上可导的任意函数f(x),若满足(x-1)f(x)0,则必有
A.f(0)+f(2)<2f(1)B.f(0)+f(2)≤2f(1)
C.f(0)+f(2)≥2f(1)D.f(0)+f(2)2f(1)
[分析]用五种数学思想进行“滚动”,最容易找到感觉应是③:分类讨论思想.这点在已条件(x-1)f'(x)≥0中暗示得极为显目.
其一,对f'(x)有大于、等于和小于0三种情况;
其二,对x-1,也有大于、等于、小于0三种情况.
因此,本题破门,首先想到的是划分讨论.
[解一](i)若f'(x)≡0时,则f(x)为常数:此时选项B、C符合条件.
(ii)若f'(x)不恒为0时.则f'(x)≥0时有x≥1,f(x)在上为增函数;f'(x)≤0时x≤1.即f(x)在上为减函数.此时,选项C、D符合条件.
综合(i),(ii),本题的正确答案为C.
[插语]考场上多见的错误是选D.忽略了f'(x)≡0的可能.以为(x-1)f'(x)≥0中等号成立的条件只是x-1=0,其实x-1=0与f'(x)=0的意义是不同的:前者只涉x的一个值,即x=1,而后是对x的所有可取值,有f'(x)≡0.
[再析]本题f(x)是种抽象函数,或者说是满足本题条件的一类函数的集合.而选择支中,又是一些具体的函数值f(0),f(1),f(2).因此容易使人联想到数学⑤:一般特殊思想.
[解二](i)若f'(x)=0,可设f(x)=1.选项B、C符合条件.
(ii)f'(x)≠0.可设f(x)=(x-1)2又f'(x)=2(x-1).
满足(x-1)f'(x)=2(x-1)2≥0,而对f(x)=(x-1)2.有f(0)=f(2)=1,f(1)=0
选项C,D符合条件.综合(i),(ii)答案为C.
[插语]在这类f(x)的函数中,我们找到了简单的特殊函数(x-1)2.如果在同类中找到了(x-1)4,(x-1),自然要麻烦些.由此看到,特殊化就是简单化.
[再析]本题以函数(及导数)为载体.数学思想①——“函数方程(不等式)思想”.贯穿始终,如由f(x)=0找最值点x=0,由f(x)>0(<0)找单调区间,最后的问题是函数比大小的问题.
由于函数与图象相联,因此数形结合思想也容易想到.
[解三](i)若f(0)=f(1)=f(2),即选B,C,则常数f(x)=1符合条件.(下图水平直线)
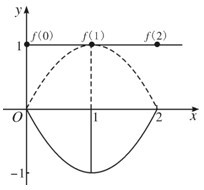
(ii)若f(0)=f(2)<f(1)对应选项A.(右图上拱曲线),但不满足条件(x-1)f(x)≥0
若f(0)=f(2)>f(1)对应选项C,D(右图下拱曲线).则满足条件(x-1)f(
[1] [2] [3] 下一页
