x）≥0.
［探索］本题涉及的抽象函数f(x)，没有给出解析式，只给出了它的一个性质：(x-1)f（x）≥0，并由此可以判定f(0)+f(2)≥f(1).自然，有这种性质的具体函
数是很多的，我们希望再找到一些这样的函数.
［变题］以下函数f(x)，具有性质(x-1)f（x）≥0从而有f(0)+f(2)≥2f(1)的函数是
A.f（x）=(x-1)3 B.f（x）=(x-1)1/2 C.f（x）=(x-1)5/3 D.f（x）=(x-1)2006/2005
［解析］对A，f(0)=-1，f(2)=1，f(1)=0，不符合要求；对B，f(0)无意义；
对C，f(0)=-1，f(2)=1，f(1)=0，不符合要求；
答案只能是D.对D，f(0)=1，f(1)=0，f(2)=1.
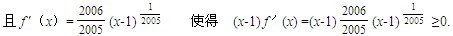
［说明］以x=1为对称轴、开口向上的函数都属这类抽象函数.如f（x）=(x-1)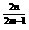
，其中m，n都是正整数，且n≥m.
［点评］解决抽象函数的办法，切忌“一般解决”，只须按给定的具体性质“就事论事”，抽象函数具体化，这是“一般特殊思想”在解题中具体应用.
［插语］这就是“滚动”的好处，解二比解一容易多了.因此，滚动开门，不仅要善于“滚到”，还要善于“滚开”.
［点评］“西瓜开门”把运动学带进了考场解题.滚动能克服解题的思维定势.
解题时，要打破思维固化，在思想方法上要“滚动”，在知识链接上要“滚动”，在基本技能技巧上也要“滚动”.总之，面对考题，在看法、想法和办法上要注意“滚动”.
●对应训练
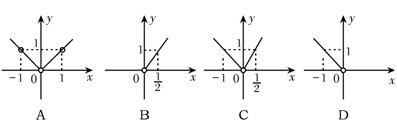
1.若动点P的坐标为(x,y)，且lgy，lg|x|，lg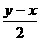
成等差数列，则动点P的轨迹应为图中的()
3.设a,b,c∈R,且4a-4b+c>0,a+2b+c<0,则下列结论中正确的是()
A.b2≤acB.b2>acC.b2>ac且a>0D.b2>ac且a<0
●参考答案
上一页 [1] [2] [3] 下一页
