1.【思考】利用题设的隐含条件.由条件知x≠0,y>0且y>x.选项B中无x<0的图像,选项D中无x>0的图像,均应否定;当x=y∈R+时,lg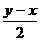 无意义,否定A,选C. 无意义,否定A,选C.
【点评】上面的解法中条件与选项一并使用,滚滚碰碰中终于找到了正确的选项.本题的常规解法是:当x≠0且y>x时,由lgy+lg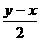 =2lg|x|,化简可得(x+y)(2x-y)=0.∴y=-x或y=2x(x≠0,y>0). =2lg|x|,化简可得(x+y)(2x-y)=0.∴y=-x或y=2x(x≠0,y>0).
2.【思考】分析各选项,仅解析式符号有区别.定义域中等号的位置有区别,所以拟从这两方面滚动着手排除错误的选项.
原函数定义域为-1≤x<0,∴其反函数值域为-1≤y<0,排除B、D.
∵原函数中f(-1)=1,∴反函数中f-1(1)=-1,即x=1时f-1(x)有定义,排除C,∴选A.
3.解析一分析四个选择支之间的逻辑关系知,若C真,则B也真;若D真,则B也真,故C、D皆假.
取符合条件4a-4b+c>0,a+2b+c<0的实数a=0,b=-1,c=0检验知选B.
解析二由选择支,联想到二次函数的判别式.
令f(x)=ax2+2bx+c,则f(-2)=4a-4b+c>0,
f(1)=a+2b+c<0,故Δ=4b2-4ac>0,即b2>ac,故选B.
【点评】在解题时易受题设条件的干扰,企图从已知不等式出发:
4b<4a+c,①
2b<-a-c,②
①×②不等号的方向无法确定,思维受阻.
用逻辑分析法和特殊值检验的方法两种方法滚动使用,简便明快,如解析一.用判别式法逻辑性强但思路难寻,如解析二.一般在做题时,为了使选择题解题速度变快,推荐学生使用解析一.
上一页 [1] [2] [3]
|
