>
1.已知函数f(x)=a1x+a2x2+a3x3+…+anxn,n∈N+,且a1,a2,…,an构成一个数列{an},满足f(1)=n2.
(1)求数列{an}的通项公式,并求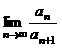 之值. 之值.
(2)证明0<f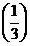 <1. <1.
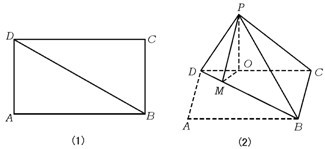
2.矩形ABCD中,AB=6,BC=2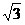 ,沿对角线BD将△ABD向上折起,使点A移到点P,并使点P在平面BCD上的射影O在DC上(如图所示). ,沿对角线BD将△ABD向上折起,使点A移到点P,并使点P在平面BCD上的射影O在DC上(如图所示).
(1)求证:PD⊥PC;
(2)求二面角P—DB—C的大小.
●参考答案
1.分析:(1){an}的各项是f(x)展开式中各项的系数,故其各项和Sn=f(1).
(2)可以预见:f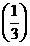 展开式的各项是系数成等差,字母成等比的综合数列,这 展开式的各项是系数成等差,字母成等比的综合数列,这
种数列的求和方法是“错项相减”.
(3)f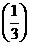 的解析式必含变量n,为判断其范围可考虑用求导法判断其单调性. 的解析式必含变量n,为判断其范围可考虑用求导法判断其单调性.
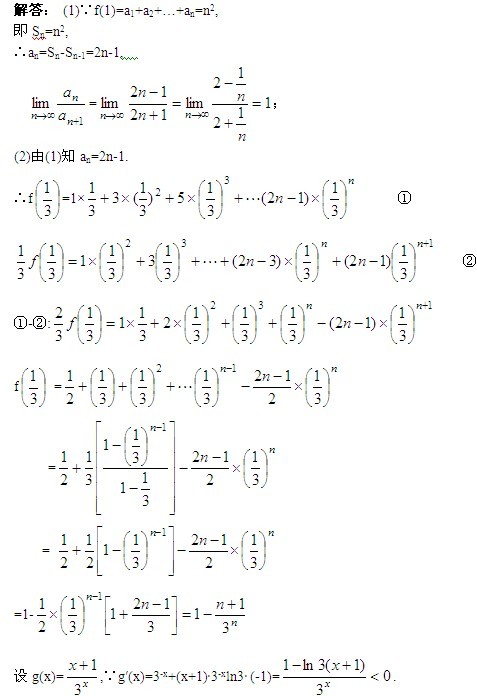

2.分析:图形经过翻折(或平移、旋转),只是位置改变,而有关线段的长度、角度及原来的平行、垂直等关系,在位置改变前后都没有改变,紧扣这一点,就能悟出解题门道.
(1)为证PD⊥PC,须先证PD⊥平面PBC,已有PD⊥PB(翻折前为AD⊥AB),还须PD⊥BC.
(2)求二面角的要点是找出二面角的平面角,已有PO⊥平面BCD于O,且O∈CD,只须作OM⊥BD即可.
解答:(1)由条件知PO⊥平面BCD于O,且O∈CD,BC⊥CD,∴BC⊥PD(三垂线定理),但PD⊥PB,∴PD⊥面PBC,从而PD⊥PC.
(2)作OM⊥BD于M,连接PM,则BD⊥PM(三垂线定理),∴∠PMO是二面角P—BD—C的平面角,

上一页 [1] [2] [3] 下一页
|
