本文摘要
问题转化是一种思维方法，将一个生疏、复杂的问题转化为熟知、简单的问题来处理,每一个具体问题如何去实现这种转化，关键是找到正确、合理的转化途径。笔者通过课堂教学实践以及对学生认为有一定难度试题的分析，发现它们都可以通过类比转化与联想转化两种途径来解决，使得深层次问题转化为浅层次问题，在平时的教学中，我们教师要重视学生在作出答案或结论之前的思维过程，引导学生探索问题转化方法，培养学生的问题转化能力。
本文关键词问题转化类比联想思维过程
一、问题的提出
在初中数学课程学习过程中，我们经常听到学生反映：上课听老师讲课，听得很懂，但到自己解题时，总感到困难重重，无从下手。事实上，有不少问题，学生感觉解答困难，并不是因为这些问题的解答太难以致学生无法解决，而是学生的思维形式与具体问题的解决存在着差异，也就是学生的数学思维存在着障碍，如何帮助学生消除这个障碍，是我们每一位数学教师必须思考的问题，也是目前我们数学教师面临的而必须去解决的问题，所以本文就如何引导学生探索问题转化的方法谈谈自己的一些做法。
二、问题转化本质和学生障碍分析
问题转化是化归思想的主要体现，问题的转化就是我们解决数学问题常用的“分析法”：要求（证）“什么”，必须先知道“谁？”，而要知道“谁”，又要求（证）“什么”？如此反复思考，最终把问题转化为已知条件或定义、定理、公式、性质等，即把深层次问题转化为浅层次问题----化未知为已知、化繁为简、化难为易、化动为静、化抽象为具体等。问题转化是一种思维方法，就是将一个生疏、复杂的问题转化为熟知、简单的问题来处理。
我对一些学生普遍认为比较难的试题作了仔细分析，发现这些题并非想象的难，它们都可以通过问题转化来解决，简单地说考查了学生数学问题的转化能力。学生思维产生障碍的根源在于：
1.审题能力、深层次分析问题能力欠缺；
2.对实际问题，应对能力不够，不会把问题进行转化、变通；
例1.陈老师要为他家的长方形餐厅(如图)选择一张餐桌，并且想按如下要求摆放：餐桌一侧靠墙，靠墙对面的桌边留出宽度不小于80cm的通道，另两边各留出宽度不小于60cm的通道．那么在下面四张餐桌中，其大小规格符合要求的餐桌编号是(把符合要求的编号都写上)．
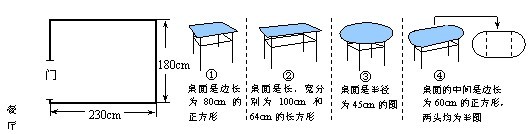
分析：此题主要是考查视图与投影知识的实际应用，但学生在答题过程中表现出来的两大思维障碍是：空间图形转化为平面图形，把实际问题转化为数学问题。答案：①②③④．
3.没有充分暴露学生解决问题时的思维过程；
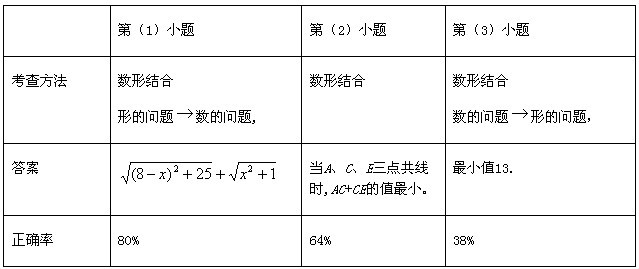
说明学生对形转化为数感觉比较容易，数转化为形比较困难，即学生对图形语言转化为符号语言比较容易接受，对符号语言转化为图形语言比较难以想象，主要是缺乏对式子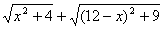
的本质意义的理解和缺乏数学建模能力的训练。
三、问题转化途径
复杂的问题如何转化为简单的问题，陌生的问题如何转化为熟悉的问题，象这样的每一个具体问题如何去实现这种转化？关键是如何寻找正确、合理的转化的途径。教学中我们可以尝试的一般有两种转化途径：联想转化与类比转化。
1.联想转化
[1] [2] [3] [4] [5] 下一页
