平时我们经常利用数形结合思想,把数和形结合起来考察,把图形问题转化为数量关系的问题,或者把数量关系的问题转化为图形问题,其实这是一种联想转化,因为我们可以找到它们的结合点,有一种特定的联系,如下面问题的解答我们可以通过图形之间的联系得到解决。
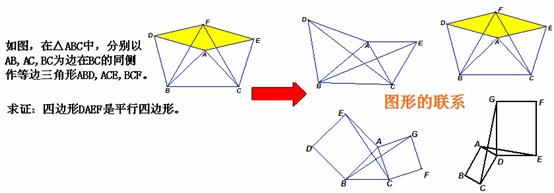
利用联想转化,可以发展学生的思维,有利于学生创新能力的培养。
联想转化使复杂问题简单化,抽象问题具体化,化难为易,获得简便易行的成功方案。我们平时经常将代数问题转化为几何问题,几何问题转化为代数问题,函数问题转化为方程问题,方程问题转化为函数问题等。
2.类比转化
初中数学,有许多概念或定理就是通过类比来学习的,类比,有纯知识的一种迁移叫类比,还有一种就是方法上的迁移也是类比,故名思异就是同类的比较学习或者说相似的知识可以有相同的本性。在教学的处理过程中,如分式的基本性质可以由分数的基本性质进行类比转化突破难点。

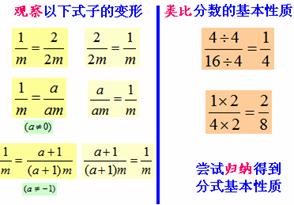
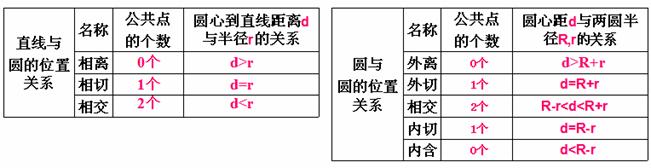
合理的类比归纳有利于数学知识的条理化、系统化,有利于数学思想方法的渗透。数学问题也可以通过类比转化,如将空间图形转化为平面图形,将简单的高次方程、分式方程、根式方程转化为一元二次方程或一元一次方程来求解,在几何教学中,我们可以类比运用研究全等三角形性质与判定的方法来学习探究相似三角形的相关性质和判定;学习正方形的性质时经常类比平行四边形、菱形、矩形的性质,如下表圆和圆位置关系类比于直线和圆的位置关系,通过类比转化,让学生把握重点并学会学习。
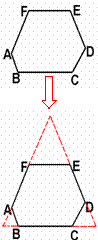
在学习多边形时,可以把多边形问题转化为三角形问题。
例3.现有一六边形铁板ABCDEF,其中∠A=∠D=
∠C=∠D=∠E=∠F=120埃?SPAN>AB=10cm,BC=70cm,CD=20cm,
DE=40cm,求AF与EF的长.
分析:六边形类比三角形,如图,六边形问题转化为三角形问题。
利用类比转化,有利于学生将知识迁移转化为能力培养,将纯知识的传授转化方法策略的渗透和掌握。
四、问题转化推广
问题转化是解决复杂问题的一种很有力的工具,在解题中,我们熟悉和掌握这一工具能使问题快速解决。对于实际问题,我们可以建立数学模型,把实际问题转化为数学问题。中学数学教学中,问题转化的应用不光体现在代数、几何中,在概率统计研究中,也可以进行图表的相互转化。
例4.A、B、C三名大学生竞选系学生会主席,他们的笔试成绩和口试成绩(单位:分)分别用了两种方式进行了统计,下表一和图一:
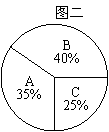
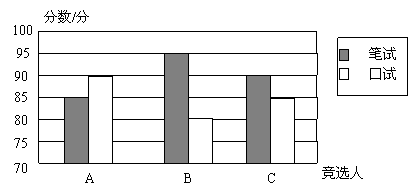
上一页 [1] [2] [3] [4] [5] 下一页
