、“问答”、“提问”都是思维训练的机会。教师在处理这些问题时,容易忽视考察学生在作出答案或结论之前的思维过程,往往使得知识的形成过程受到高度压缩,学生不注重理清知识的来龙去脉,忽视分析、探索过程,结果造成学生思维空间狭小、思维闭塞,致使生搬硬套结论,采用题海战术,甚至机械模仿套路与模式。教师必须重视学生的思维活动,教学过程中要充分暴露学生错误的想法。思维的训练和发展是以暴露思维过程为前提的,学生的思维能力是在暴露的过程中得到锤炼和提高的。
3.引导学生探索问题的方法
正向思维法----是从已知到结论的思考问题方法,是解决问题最常用的一种思维方式;
逆向思维法----是背逆通常思考问题方法,寻求解决问题的一种思维方式;
多维发散法----多维发散法指在研究问题时,从某一信息出发,通过多角度、多层次、多形式的命题变换,形成立体的思维网路,从而产生新问题、新信息的思维方法。在数学教学中,多维发散的思路主要有:①条件发散,②解法发散,③分析发散,④迁移发散,⑤创造发散等。
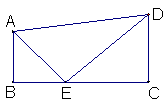
例5.如图,梯形ABCD中,AB∥DC,∠B=90埃?/SPAN>E为BC上一点,且△ABE与以C、D、E为顶点的三角形相似。
(1)若BC=8,AB=3,DC=4,求BE的长;
(2)若BC=4,AB=3,DC=4,求BE的长;
(3)若BC=6,AB=3,DC=4,求BE的长;
(4)请对以上结果的原因进行分析。
分析:前三小题,可设BE为X,学生通过列比例式把几何问题转化为代数问题,即把求BE的长度问题转化为解关于X的方程问题,并进行分类讨论。
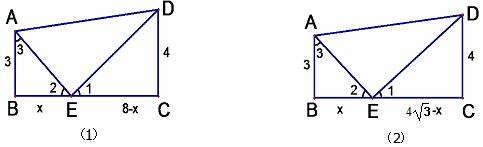

第(4)题就是培养学生的发散性思维,对前三题为什么会有两种情况以及什么时候BE出现3个答案,2个答案,1个答案用图形语言来描述很清晰,引导学生把数、式的问题转化为形的问题,同时揭示本题的几何意义。
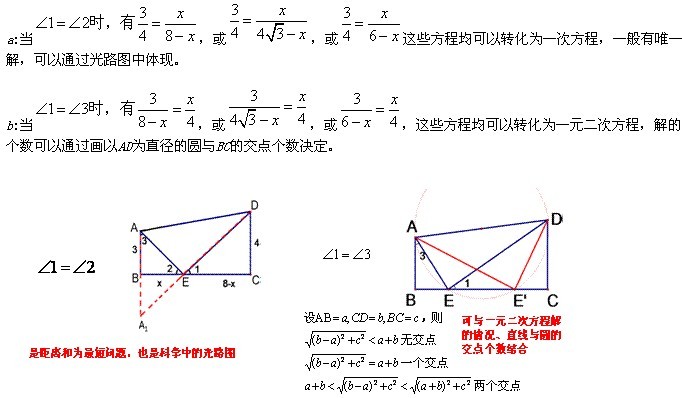
本题包含了条件发散,迁移发散,创造发散等思维方式。
在解决某一具体问题时,我们可选择其中的部分思维方式对学生进行训练。让学生学会常用的解决问题的途径与方法,养成乐于思考,勇于探索的精神,让学生真正把书读活,从知识立意转向能力立意,我们教师真正把书教活,从教会知识转向发展智慧。平时加强对学生观察、分析、迁移、反思、创新能力的培养,关注知识的生长点,引导学生揭示数学本质问题,学会问题合理转化,加强方法引导,授之以渔,注重培养学生的创新思维能力。
结束语
数学解题的过程是不断转化问题的过程,不断地把未知问题转化为已知问题,把陌生问题转化为熟悉问题、把繁杂问题转化为简单问题。问题的内部结构和相互之间的联系,决定了处理这一问题的方式、方法,因此我们在平时的教学中,要把学习内容问题化、数学化,要充分揭示问题间的内部联系,暴揭露学生问题转化时的思维过程,正确引导学生探索问题转化方法,发展学生问题转化能力,促进学生的终身学习。
参考文献:
宋小妹《转变学习方式,培养学生解决问题的能力》
相卫东《探索解题方法突出思维训练》
上一页 [1] [2] [3] [4] [5] 下一页
|
