作为抽象函数的重要内容,对称性和周期性的关系经常都是考察的重点,记住一句话“同号看周期,异号看对称”能解决很多问题,具体内容我就不说了,请参考文章《函数周期性与对称性的关系》,提炼出里面核心的两句话便是:
若函数f(x)有两条对称轴x=a和x=b(a≠b),那么该函数一定为周期函数,且其中一个周期为2|a-b|
若函数f(x)有两个对称点(a,c),(b,c),那么该函数一定为周期函数,且其中一个周期为2|a-b|
若函数f(x)有一条对称轴x=a和一个对称点(b,c),那么该函数一定为周期函数,且其中一个周期为4|a-b|
大伙可以自己尝试去证明这些结论。学夫子在这里想重新对此说明两条,是我们容易犯错,也容易忽略的内容。
一:这些结论一不小心就容易简化为:
若一个函数有两个对称性(不管是轴对称函数中心对称),则其一定为周期函数。
如果有一个判断题是如此讲述,那就是大错特错,函数有两条对称轴,不一定就具有周期性,除非加上这两条对称轴都是垂直于X轴,也就是形如x=a这样的对称轴;一个函数有两个对称点,那也不一定就具有周期性,除非这两个对称点的纵坐标都相等。有一个最简单不过的例子就是函数y=x,下图:
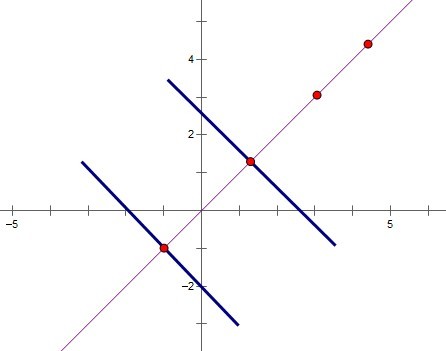
很容易知道,图象上的每一个点都是函数的对称点,显然,该函数没有周期性。该图象的任何一条法线(即垂直于y=x的直线)都是函数的对称轴,该函数没有周期性。这是我们在理解对称性与周期性时需要注意的。
二:注意变化后的对称性周期性条件
永远把握住“同号看周期,异号看对称”这一句话,结合前面的结论,便可以解决这一类问题。只要题目当中给出F(f(x+a),f(x+b))=0,那基本上都是间接告诉你该函数的周期;若给出F(f(x+a),f(-x+b))=0,那基本上也是间接告诉对称性的。这就需要我们对给出的条件进行化简,使之变成与周期性和对称性有关的式子。一般的方法是在f(x+a)与f(x+b)中的x同时加上|a-b|,多化简几步,自然就能化简出来。
如:函数f(x)对任意x满足f(x+2)=1/f(x)。这条件是同号的,铁定跟周期性有关,这就需要我们对其进行化简,同时在括号里加上2得到:
f(x+4)=1/f(x+2)=f(x),说明该函数是以4为周期。
又如:f(x+2)(1-f(x))=1+f(x)。这条件也是同号的,也是和周期有关。我们对括号里的同时加上2得到:
f(x+4)(1-f(x+2))=1+f(x+2),将f(x+2)=(1+f(x))/(1-f(x))带入化简得到:
f(x+4)=-1/f(x),还是没有得到我们想要的结果,那就进一步对括号里的同时加上4,得到:
f(x+8)=-1/f(x+4)=f(x)。说明还是是以8为周期。
当然题目是说不完的,具体思路就是如此。抽象函数因为他的抽象让人头疼,但也恰好是其抽象性使得我们有更多的发挥空间。(来源:学夫子数学博客)
|
