培养学生数学阅读能力的一般方法

利于学生主动地进行观察、实验、猜测、验证、推理与交流等数学活动．”在“教学建议”中指出：“有效的数学学习过程不能单纯地依赖模仿与记忆，教师应引导学生主动地从事观察、实验、猜想、验证、推理与交流等数学活动，从而使学生形成对数学知识的理解和有效的学习策略，”可见，数学教学应重视观察、探究、实验等活动．面临的问题是在引导学生参与这些活动时，往往需要有较长篇幅的文字材料出现，学生在这些材料的引导下，需要从事多项数学活动，在参与这些活动的过程中却不一定能抽象概括出“活动”的目的或本质内容．
　　
　　案例2勾股定理的发现过程，
　　
　　勾股定理本身的结论非常简洁，而且容易记忆，如果直接告诉学生，几分钟就可以解决问题，但这样的教学留给学生的知识只是一个数学符号，学生不知道为什么要研究勾股定理，而且丢失了一次培养学生探究学习的好机会，对于这个定理，大部分教师都是通过创设一定的问题情境，引导学生在实验操作的过程中自主探究，从而得到定理的．下面的设计就是很好的一例．
　　

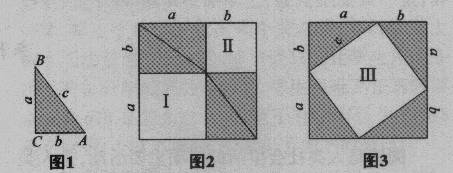
　　(1)用硬纸板剪8个如图1所示的同样大小的直角三角形，设直角三角形的直角边长分别为a和b，斜边长为c；
　　
　　(2)在白纸上画出两个边长均为（a+b）的正方形；
　　
　　(3)如图2所示，将已经剪出的4个直角三角形，摆放在第一个正方形内；
　　
　　(4)如图3所示，将另外的4个直角三角形，摆放在第二个正方形内．
　　
　　(5)观察图2与图3，并思考两个图中三个小正方形I、Ⅱ、Ⅲ的面积之间有怎样的关系？
　　
　　该设计的意图是在以上问题的引导下，让学生通过操作、观察、对比等活动，探索得到结论：a2+b2=c2．这个结论就是勾股定理．然而，在具体实施过程中，由于有些学生的抽象概括能力不高，难以实现教师的预设．这个案例告诉我们：数学阅读需要具有较强的抽象概括能力，这是数学阅读的又一特点．
　　
　　3．阅读时不能进行逻辑推理活动
　　
　　数学是一门建立在公理体系基础上，一切结论都需要严格加以证明的学科．数学推理的严格性和
　　
　　数学结论的确定性是大家所共知的．学生在阅读教科书中的概念、性质、法则、公式以及解题方法、操作步骤时，一刻也离不开逻辑推理活动，然而现实状况却是，许多学生在进行数学阅读时，逻辑推理活动却不能很好地渗透在阅读活动之中，
　　
　　案例3在不是有理数．
　　
　　青岛·泰山版课标教材八年级上册在“加油站”栏目中提供了一个阅读材料，内容如下：
　　

　　
　　教科书在这段阅读材料中，利用反证法证明了在既不是整数，也不是分数，为探索它是一个无限不循环小数奠定了理论基础，在这里渗透了推理论证的思想，但由于学生缺乏推理论证过程的训练，推理论证能力不高，造成了阅读理解上的困难，由此可见，数学阅读的过程中，往往渗透着推理论证的思想．
　　
　　二、培养学生数学阅读能力的一般做法
　　
　　现在有这样一种现象：教师上课不用教科书，只用习题纸．特别是在各种公开课、示范课、讲课比赛中，似乎已成为一种风气．表面看来，这样的课教学过程顺畅，教师“导”的精彩，学生“演”的投入，但这种教法忽略了学生阅读的环节，更谈不上培养学生的阅读能力了．事实上，数学学习一刻也离不开阅读，在数学教学中，重视阅读至少有以下几点好处：
　　
　　(1)拓展学生的知识面；
　　
　　(2)澄清模糊观念；
　　
　　(3)加强对知识之间相互联系的认识；
　　
　　(4)培养学生的思维能力；
　　
　　(5)提高学生解决实际问题的能力；
　　
　　(6)帮助学生感悟数学思想方法；
　　
　　(

上一页 [1] [2] [3] [4] [5] 下一页