【原题】:已知P是△ABC内一点,且满足“向量PA+2向量PB+3向量PC=零向量”记△ABP,△BCP,△ACP的面积依次是S1,S2,S3,则S1:S2:S3等于___________答案:3:1:2
本题其实是一个竞赛题结论的推广,在这里就不写基于本题的解决过程了,干脆直接来解析有关这一类问题的通用解题方法以及推广后的结论,不会做题不是你的错,但是第二次不会做相同的题就是你的不对。
解析:现在我们直接来证明这样的一个结论,△ABC内有一点P,设CP所对的三角形PAB的面积为SC,PBC的面积为SA,APC的面积为SB,则有下面的结论成立:
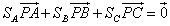
这个结论的另一种表述方法是:若存在正数k,m,n使得
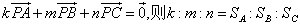
显然这两种说法是等价的(取决于平面向量基本定理的成立),现在我们证明第二种形式的结论成立,假设k,m,n都是小于1的,即我们在下图得到的三角形A'B'C'在三角形ABC内部,方便我们的处理,当k,m,n大于1的时候,我们一方面可以两边同时除以一个k+m+n,使得系数小于1,二来这时候的三角形A'B'C'在三角形外部,处理的方法和内部也是一样的:

来源:学夫子数学博客
