江西省安福县城关中学 曹经富
“课题学习”类试题在近年各地中考试题中频频出现,此类题型特点鲜明、内容丰富、超越常规,源于课本,又高于课本,不仅注重数学实践应用、动手探究的培养,还关注学生学习的过程和思想方法的渗透.这类试题较好地考查了学生的阅读理解能力、知识迁移能力和分析问题、解决问题的能力,这无疑为课堂教学注入了新鲜的活力。它既是一项全新的课程内容.又是一种具有现实性、问题性、实践性、综合性和探索性的新型的学习活动.经常成为呈现中考数学知识和能力的载体。现结合2011年各地中考题进行说明,希望能给大家带来一定的启示与帮助.
一、情景问题拓展类
例1:(2011江苏盐城)情境观察
将矩形ABCD纸片沿对角线AC剪开,得到△ABC和△A′C′D,如图1所示.将△A′C′D的顶点A′与点A重合,并绕点A按逆时针方向旋转,使点D、A(A′)、B在同一条直线上,如图2所示.观察图2可知:与BC相等的线段是,∠CAC′=?/SPAN>.
问题探究
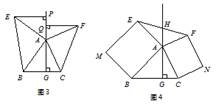
如图3,△ABC中,AG⊥BC于点G,以A为直角顶点,分别以AB、AC为直角边,向△ABC外作等腰Rt△ABE和等腰Rt△ACF,过点E、F作射线GA的垂线,垂足分别为P、Q.试探究EP与FQ之间的数量关系,并证明你的结论.
拓展延伸
如图4,△ABC中,AG⊥BC于点G,分别以AB、AC为一边向△ABC外作矩形ABME和矩形ACNF,射线GA交EF于点H.若AB=kAE,AC=kAF,试探究HE与HF之间的数量关系,并说明理由.
思路点拨:沿矩形的对角线剪开所得的两个三角形是全等的,由如图2中位置及全等关系可得BC=AD,∠CAC′=90?/SPAN>;在图3中,当等腰Rt△ABE和等腰Rt△ACF的直角顶点重合于直线GP上的点A时,构建了如图2所示的两个直角三角形全等的数学模型,即Rt△ABG≌Rt△EAP.Rt△ACG≌Rt△FAQ,进而得到AG=EP,AG=FQ,从而得到EP=FQ.在图4中,当背景由等腰直角三角形变为矩形时,但矩形的长与宽之比均为k,从而构建了如图2所示的两直角三角形相似(全等)的数学模型,借助相似比及Rt△EPH≌Rt△FQH.容易得出HE=HF。
解:情境观察AD(或A′D),90
问题探究结论:EP=FQ.证明:∵△ABE是等腰三角形,∴AB=AE,∠BAE=90?
∴∠BAG+∠EAP=90?∵AG⊥BC,∴∠BAG+∠ABG=90?/SPAN>,∴∠ABG=∠EAP.
∵EP⊥AG,∴∠AGB=∠EPA=90?/SPAN>,∴Rt△ABG≌Rt△EAP.∴AG=EP.
同理AG=FQ.∴EP=FQ.
拓展延伸结论:HE=HF.理由:过点E作EP⊥GA,FQ⊥GA,垂足分别为P、Q.

∵四边形ABME是矩形,∴∠BAE=90?/SPAN>,
∴∠BAG+∠EAP=90?AG⊥BC,∴∠BAG+∠ABG=90?/SPAN>,
∴∠ABG=∠EAP.∵∠AGB=∠EPA=90?/SPAN>,∴△ABG∽△EAP,
∴=.同理△ACG∽△FAQ,∴=.
∵AB=kAE,AC=kAF,∴==k [1] [2] [3] [4] 下一页
|
