,∴=.∴EP=FQ.
∵∠EHP=∠FHQ,∴Rt△EPH≌Rt△FQH.∴HE=HF
点评:本题以课题学习的方式呈现,解决此题的关键在于简单情景入手,准确把握相关图形的特征与模型,透过现象看到数学活动问题的本质(直角顶点重合于直线上某一点时,酝酿与构建了两直角三角形全等或相似关系),不被“动”及“变化的图形”所迷,关键是在于由特殊到一般、由简单到复杂的思维方式,这类试题不仅结论可以类比,而且思维方法、证明过程及说理过程也可通过类比得出,这种模式应引起我们的重视与关注。
二、阅读理解类
例5:(2011湖南永州)探究问题:
⑴方法感悟:
如图①,在正方形ABCD中,点E,F分别为DC,BC边上的点,且满足∠EAF=45?/SPAN>,连接EF,求证DE+BF=EF.
感悟解题方法,并完成下列填空:
将△ADE绕点A顺时针旋转90?/SPAN>得到△ABG,此时AB与AD重合,由旋转可得:
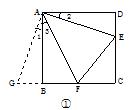
AB=AD,BG=DE,∠1=∠2,∠ABG=∠D=90?
∴∠ABG+∠ABF=90?90?180?/SPAN>,
因此,点G,B,F在同一条直线上.
∵∠EAF=45?nbsp;∴∠2+∠3=∠BAD-∠EAF=90?45?45?/SPAN>.
∵∠1=∠2,∴∠1+∠3=45?/SPAN>.
即∠GAF=∠_________.又AG=AE,AF=AF
∴△GAF≌_______.
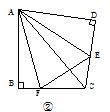
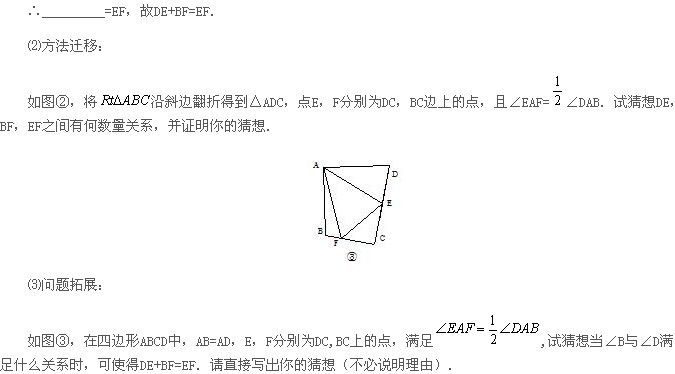


点评:此题以阅读理解的形式进行课题学习探究,题目中首先提供某种思路、方法或中间步骤,探讨某种情境或特殊情形下的解题思路与方法,然后将其进行拓展、推广到一般情况,进一步探究相关结论,解答此类问题的基本步骤是阅读——分析——理解——迁移——创新应用。
三、操作探究类
例3:(2011江苏苏州)如图①,小慧同学吧一个正三角形纸片(即△OAB)放在直线l1上,OA边与直线l1重合,然后将三角形纸片绕着顶点A按顺时针方向旋转120?/SPAN>,此时点O运动到了点O1处,点B运动到了点B1处;小慧又将三角形纸片AO1B1绕B1点按顺时针方向旋转120?/SPAN>,点A运动到了点A1处,点O1运动到了点O2处(即顶点O经过上述两次旋转到达O2处).
小慧还发现:三角形纸片在上述两次旋转过程中,顶点O运动所形成的图形是两段圆弧,即弧OO1和弧O1O2,顶点O所经过的路程是这两段圆弧的长度之和,并且这两端圆弧与直线l1围成的图形面积等于扇形AOO1的面积、△AO1B1的面积和扇形B1O1O2的面积之和.
上一页 [1] [2] [3] [4] 下一页
