“平移”是坐标平面内经常用到的数学思想。平移主要考虑两个内容:一是平移的方向,而是平移的距离。如果知道这两个内容,就可以得出某一个点经过平移后所得到的点的坐标。

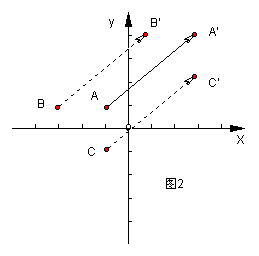
例1、如图所示,三架飞机A、B、C保持编队飞行,飞行10分钟后,飞机A飞行到A’的位置,此时飞机B、C飞到的位置的坐标分别是。
(已知A(-1,1),B(-3,-1),C(-1,-1),A’(4,3))
分析:飞机A的坐标是(-1,1),飞到的位置A’的坐标是(4,3),利用平移的思想进行考虑,可以认为飞机A先向右平移4个单位长度,然后再向上平移3个单位到达点A’的位置。题目中已经说明三架飞机保持编队飞行,所以飞机B、C飞行到的位置也就符合上述的平移变换。所以飞机B飞行到的位置B’就相当于先向右平移4个单位长度,然后再向上平移3个单位,飞机C飞到的位置也是如此(如图2所示)。
答:飞机B飞到的位置B’的坐标是(4,1),飞机C飞到的位置C’的坐标是(2,3)。
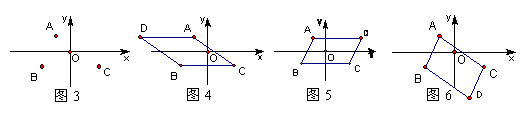
例2、如图3所示在平面直角坐标系中,有以下几点:A(-3,4)、B(-6,-2)、C(6,-2)。如果以A、B、C为顶点,作一个平行四边形,试写出第四个顶点的位置坐标。
分析:
如果一个平行四边形已知其中的三个顶点,求第四个顶点的位置,可以有三种情况,所以本题目中的第四个点D的位置有图4、图5、图6三种情况。本题的难点不是如何确定第四个顶点的数量,而是如何求出第四个顶点的坐标。根据平行四边形的特点,可以利用平移的思想进行考虑。
例如图4中点D的得出可以通过点A的平移来判断,平移的距离相当于BC的长度,因为CB与AD平行,所以平移的方向相当于从点C到点B的方向。点B相当于点C向左平移12个单位长度得到的,所以点A也向左平移12个单位长度就可以得到点D,因为点A的坐标是(-3,4),所以点D的坐标是(-15,4)。图5中点A的平移过程相当于从点B到点C的平移过程,图6中点B的平移过程相当于从点A到点C的平移过程。
解:第四个顶点D的坐标可以有三种情况,分别是:(-15,4)或(9,4)或(3,-8)。
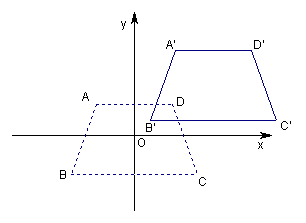
练习:四边形ABCD在直角坐标系中各顶点的坐标如下:A(-2,2),B(-3,-2),C(3,-2),D(2,2)。如果把四边形ABCD平移到A’B’C’D’的位置,平移后点A’的坐标是(2,5),求出其他各点B’、C’、D’的坐标。
巧用平移妙解面积问题
求解与长方形有关的面积是日常生活、生产中常见的问题之一,解决这类问题有一种巧妙的方法那就是采用平移.通过平移,使分散、零碎的图形得以集中,从而方便运用整体思想进行求解.
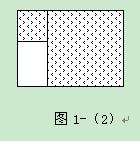
例1如图1-1是小明家一个长方形花坛,空白部分准备用于种花,种草部分分别是一大一小的正方形.已知大正方形的面积为49平方米,小正方形的面积为9平方米.问种花的面积是多少平方米?
[1] [2] [3] [4] [5] 下一页
