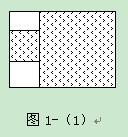
析解:采用平移,将小正方形向上平移到边缘,如图1-2所以.由已知易得种花部分是长方形,长为大正方形的边长减去小长方形的边长,即7-3=4(米),宽恰好是小正方形的边长3米.因此,种花的面积为3×4=12(平方米).
想一想:如果图形不加处理,解题思路又是怎样的呢?
例2如图2-1,某小区规划在一个长为AD=40米,宽为AB=26米的长方形场地ABCD上,修建三条宽都是2米的小路,其中两条与AB平行,另一条与AD平行,其余部分种草.问种草区域的面积是多少?
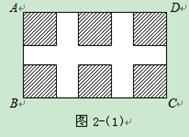
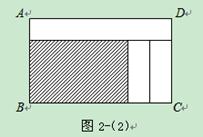
析解:将图2-1的小路分别沿BA,BC平移到如图2-2所示的位置,则易知种草的长方形的长为40-2×2=36(米),宽为26-2=24(米),所以,种草区域的面积为36×24=864(平方米).
想一想:如果图形不加处理,分别求出三条小路的面积,然后用场地的总面积减去三条小路的面积,求得种草区域的面积.与运用平移来解,感觉怎样?
例3如图3-1所示,在一块长为24米,宽为16米的草坪上有一条宽为2米的曲折小路,你能运用你所学的知识求出这块草坪的绿地面积吗?
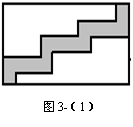

析解:小路的面积只与小路的宽度和长度有关,与其位置没有关系.可以将路分解成向下和向右分别平移的两部分,平移后如图3-2所示.这时,绿地转化为长22米,宽18米的长方形,可求得绿地的面积为:22×18=396(平方米).
想一想:直接求小路的面积是无法求解的,
那么,本题中将曲折的小路进行平移,意义何在?
图形的平移在解题中的应用
平移是图形的一种重要变换.在实际解题中,若我们能恰当地运用图形的平移变换,往往能起到集中条件、开阔思路、化难为易、出奇制胜的效果.请看下面几例:
一、变换图形的形状的问题.
例14根火柴棒形成如图所示的象形“口”字,平移火柴棒后,原图形能变成的象形汉字是()
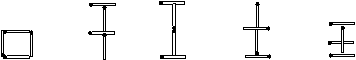
A. B.
上一页 [1] [2] [3] [4] [5] 下一页
