解析:利用“平移不改变图形的形状和大小”这一性质可使本题迅速解决.由图形可知,图1(a)和图1(b)的阴影部分经过平移可以组成一个长方形,如图1(c).则图1(a)中的长为a,宽为(b-1),所以面积为:a(b-1)=ab-a;图1(b)中的长为a,宽为(b-1),所以面积为:a(b-1)=ab-a.
说明:这里通过平移的知识,使求解简洁、方便.
例2.如图2,在高为2米,水平距离为3米楼梯的表面铺地毯,地毯的长度至少需米.
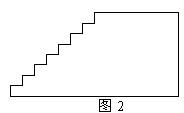
解析:把每阶楼梯的高沿水平方向平移,和就是楼梯的总高度;
把每阶楼梯的宽沿竖直方向平移正好构成了楼梯的总长度,
再把楼梯的总高度和总长度相加,即得地毯的长度至少需2+3=5(米).
例3.如图3,从A地到B地经过一条小河(河岸平行),今欲在河上建一座桥,应如何选择桥的位置才能使从A地到B地的路程最短?
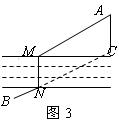
解析:从A到B要走的路线是A→M→N→B,如图3,而MN是定值,于是要使路程最短,只要AM+BN最短即可.此时两线段应在同一平行方向上,平移MN到AC,从C到B应是余下的路程,连结BC的线段即为最短的,此时不难说明点N即为建桥位置,MN即为所建的桥.
例4.“小小竹排江中游,滔滔江水向东流……”这首歌是那样熟悉、那样亲切,现在我们来研究一个关于竹排的问题.如图4,静止的湖面上,西南风将一块四边形的竹排以每分钟0.5米的速度向前推进,问10分钟后此竹排沿着什么方向平移了多少米?画图表示.

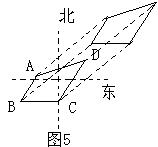
解析:由题意可知,竹排平移的方向为西南风的方向即北偏东45?/SPAN>,竹排平移的距离为0.5×10=5(米).画图如图5所示.
说明:由平移的特征可知,对应线段平行且相等.对应点的连线平行且相等.此题通过实际问题体验平移现象,理解平行特征,结合方向角、行程计算,认识知识之间的联系,不可孤立看问题.
生活中利用平移解决问题的例子还有很多,如室内地面砖图案,电梯上下移动,火车在笔直的铁轨上飞驰等都采用了平移变换的思想,给生活带来了方便.(来源:凤凰数学网)
上一页 [1] [2] [3] [4] [5]
