作者:佚名
“旋转”是现实生活和生产中广泛存在的现象,是现实世界运动变化的最简捷的形式之一,它不仅是探索图形一些性质的必要手段,而且也是解决现实世界中的具体问题以及进行数学交流的重要工具.在近几年的中考试题中,以图形为载体、以旋转为手段考查同学们操作、想象、探究能力的中考题层出不穷,今举数例,供参考.
例1:如图1,把正方形ACFG与Rt△ACB按如图(甲)所示重叠在一起,其中AC=2,∠BAC=600,若把Rt△ACB绕直角顶点C按顺时针方向旋转,使斜边AB恰好经过正方形ACFG的顶点F,得△A′B′C′,AB分别与A′C,A′B′相交于D、E,如图(乙)所示.
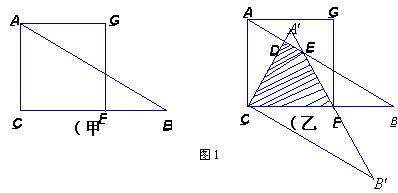


⑴.△ACB至少旋转多少度才能得到△A′B′C′?说明理由.
⑵.求△ACB与△A′B′C′的重叠部分(即四边形CDEF)的面积(若取近似值,则精确到0.1)
例3:如图3-1,一等腰直角三角尺GEF的两条直角边与正方形ABCD的两条边分别重合在一起.现正方形ABCD保持不动,将三角尺GEF绕斜边EF的中点O(点O也是BD中点)按顺时针方向旋转.



(1)如图3-2,当EF与AB相交于点M,GF与BD相交于点N时,通过观察或测量BM,FN的长度,猜想BM,FN满足的数量关系,并证明你的猜想;
(2)若三角尺GEF旋转到如图1-3所示的位置时,线段FE的延长线与AB的延长线相交于点M,线段BD的延长线与GF的延长线相交于点N,此时,(1)中的猜想还成立吗?若成立,请证明;若不成立,请说明理由.
分析:本题主要考查旋转图形的性质,解答时应着眼于图形的旋转不变性来探索线段之间的变化规律.对于(1)问,经测量后可知BM=FN.然后利用三角形全等证明即可;对于(2)问,要明确,在继续旋转的过程中,虽然△OBM和△OFN都发生了变化,但二者之间全等的关系没变.故结论成立.
解:(1)BM=FN.
证明:∵△GEF是等腰直角三角形,四边形ABCD是正方形,
∴∠ABD=∠F=45?/SPAN>,OB=OF.
又∵∠BOM=∠FON,∴△OBM≌△OFN.
∴BM=FN.
(2)BM=FN仍然成立.
证明:∵△GEF是等腰直角三角形,四边形ABCD是正方形,
∴∠DBA=∠GFE=45?/SPAN>,OB=OF.∴∠MBO=∠NFO=135?/SPAN>.
[1] [2] [3] 下一页
