又∵∠MOB=∠NOF,∴△OBM≌△OFN.
∴BM=FN.
评注:本题利用图形旋转的不变性,探索图形在旋转过程中的有关规律,让同学们体验图形旋转变换的性质,同时也考查了同学们空间想象、规律探索、推理能力以及分析问题、解决问题的能力,是一道不可多得的优秀题目.
例4已知∠AOB=900,在∠AOB的平分线OM上有一点C,将一个三角板的直角顶点与C重合,它的两条直角边分别与OA、OB(或它们的反向延长线)相交于点D、E.
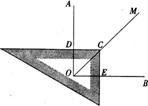
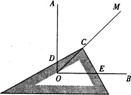
当三角板绕点C旋转到CD与OA垂直时(如图4-1),易证:OD+OE=OC.
当三角板绕点C旋转到CD与OA不垂直时,在图4-2、图4-3这两种情况下,上述结论是否还成立?若成立,请给予证明;若不成立,线段OD、OE、OC之间又有怎样的数量关系?请写出你的猜想,不需证明.
分析:由于在旋转的过程中,虽然点O的位置发生了变化,但∠AOC和∠COE的大小不变,都是45?/SPAN>,因此可过C分别作OA、OB的垂线,从而转化为等腰直角三角形(图4-1)来处理.对于图4-3可仿图2处理.
解:图4-2结论:OD+OE=OC.
证明:过C分别作OA、OB的垂线,垂足分别为P、Q.
△CPD≌△CQE,DP=EQ.
OP=OD+DP,DQ=OE-EQ.
又OP+0Q=0C,即OD+DP+OE-EQ=0C.
∴OD+OE=0C.
图4-3结论:OE-OD=OC.
评注:从以上两例可以看出,解决这类问题的关键是要把握以下两点:
1.在解题时,认真观察图形,不放过一个细节,看清旋转的角度和方向,找准旋转前后的相关的角与边,在旋转的过程中,弄清变与不变的量;
2.再解决这类问题时,我们通常将其转换成全等形求解,根据旋转变换的特征,找到对应的全等形,通过线段、角的转换达到求解的目的.
旋转出的探究规律题
在近几年的考题中,探究性题目无处不在,它的呈现形式也是千姿百态,下面我们就聚焦以正方形为载体,旋转出的探究规律题。
例1:如图①所示,已知两个全等正方形ABCD与A1B1C1D1,正方形ABCD的点C与正方形A1B1C1D1的中心重合,且绕点C旋转.
(1)当正方形ABCD旋转至图②时,两个阴影部分的面积是否相等?说明理由。(2)当正方形ABCD旋转至任意位置时,如图③,重叠部分的面积会怎样变化?说明你的结论.
(3)观察所示三个图形,被覆盖住的正方形的边长情况,结合(1)(2)把该图形所蕴涵的规律用简洁的语言表述出来。
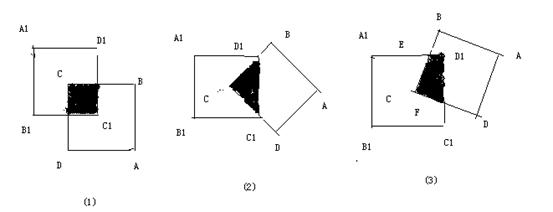
解析:本题以正方形为载体,通过一个正方形绕另一个正方形的中心旋转而引发出的一系列探究性问题,观察图(1)和图(2)这两种特例可知阴影部分面积等于其中任意一个正方形面积的1/4,所以两个阴影部分
上一页 [1] [2] [3] 下一页
