的面积相等;在图(3)的一般情形下,在探究其蕴涵的规律,此时,应联想上面的两种特例,转化为(1)(2)的情形,可以过C点向正方形A1B1C1D1的A1D1和C1D1,引垂线或连结CD1和CC1,借助全等,仍得出阴影部分面积等于其中任意一个正方形面积的1/4,再观察被覆盖住边的情形,图(1)和图(2)这两种特例中,被覆盖住的边长和正方形的边长相等,图(3)的情形,由上面的方法,运用全等,可知被覆盖住的边长始终等于正方形的边长。把这两条规律结合起来就是第三问的答案了。
例2:如图—1、图—2分别是两个相同正方形、正六边形,其中一个正多边形的顶点在另一个正多边形外接圆圆心0处.
(1)求图—1中,重叠部分面积与阴影部分面积之比;
(2)求图—2中,重叠部分面积与阴影部分面积之比(直接写出答案);
(3)根据前面探索和图13—3,你能否将本题推广到一般的正n边形情况(n为大于2的偶数)?若能,写出推广问题和结论;若不能,请说明理由.
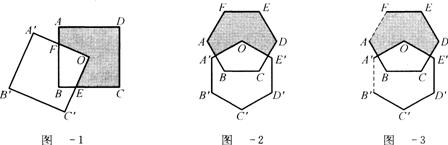
解析:本题与上面的题目相类似,由上面题目中的规律易得出图—1中,重叠部分面积与阴影部分面积之比1:3,在图2中,连结BO、DO,借助三角形的全等,也可以清晰发现重叠部分面积与阴影部分面积之比1:2,自己还可举一个正八边形的例子得出的结论,在此基础上观察比值的规律就得到了(n-2):(n+2).(来源:凤凰数学)
上一页 [1] [2] [3]
