中心环节.为了得到问题的解法,应该拟订一个计划.
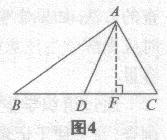
对于此例,可以看到,目标的特点非常突出,是中线和三边的平方之问的关系.那么,哪些知识与边的平方有联系呢?于是便很容易联想到勾股定理.要使用勾股定理,只需作辅助线AF⊥BC,垂足为点F(如图4),构造直角三角形就可以了.

根据以上的分析,可以拟定此题的解题计划:
①作辅助线A,上BC,垂足为点F;
②建立关系式①和②;
③消去DF,整理成目标的形式.
(3)整理叙述,实行计划.
探索得到解法之后,要认真地加以整理,用确切的数学语言将解题过程表述出来.在表述的过程中,要求层次分明、条理清晰、文字精炼、格式规范、合乎逻辑,并仔细地检查每一个步骤.
对于此例,在实行计划时,应分为两种情况:
①当AB≠AC时,不妨设AB>AC作AF⊥BC,垂足为点F(如图4).
则在Rt△BFA和Rt△DFA中,由勾股定理,得
(4)回顾反思,检查验算.
这是解题的最后一个环节,检查验算主要是看结果是否正确,推理是否合乎逻辑,步骤是否完整,以便及时地查漏补缺,纠正错误.
回顾此例,因为是证明题,所以只需保证每一步推理的正确性.检查推理的每一步,依据都很充分,从讨论上看,没有遗漏的情况,因而是正确的.
在解题教学中,如果能长期坚持这样的训练,学生的解题能力必将得到较大的提高.教师在解题教学中,可以依此策略,将重点放在引导学生探索解法上,在学生探索得到解法之后,要鼓励他们进行讨论、相互交流,而不要直接由教师进行讲解,否则,就会出现“学生学得快,忘得更快”的现象.
策略3:在数学性质(定理)的教学过程中,应重点引导学生分清它们的条件和结论,理解抽象、概括或证明的过程
在数学性质(定理)的教学过程中,应引导学生弄清它们的来源,分清它们的条件和结论,理解抽象、概括或证明定理的过程,从而让学生做到“既知其然,又知其所以然”.
在探求证明的过程中,可采用直观操作和推理论证相结合的方式.
案例3“两组对边分别相等的四边形是平行四边形”的发现与证明过程.
“两组对边分别相等的四边形是平行四边形”是平行四边形的判定定理之一,是在学生操作实验
的基础上得到的,教学中,应要求学生进行动手操作(剪、拼、接三角形硬纸片),并把论证作为学生探索活动的自然延伸和必要的发展,让学生在拼接三角形硬纸片的过程中,发现证明该定理的思路.
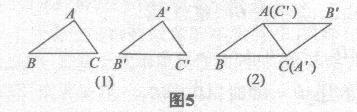
(1)剪两个同样大小的三角形硬纸片△ABC,△A’B’C’(三边都不相等);
(2)用这两个三角形拼成四边形,观察所得到的四边形的特点,你能得到怎样的猜想?相互交流自己的想法;
(3)证明所得到的猜想,将其归纳成一般结论.
学生进行的操作过程如图5所示:

上一页 [1] [2] [3] [4] [5] 下一页
